|
![]()
Geometría
Cuerpos Redondos
Una lata de refresco, la punta de un lapicero y un balón son cuerpos geométricos que tienen parte de su superficie, o toda ella, curva. La lata es un cilindro, la punta del lápiz es un cono y el balón una esfera. A estos tres cuerpos, cilindro, cono y esfera, se les llama cuerpos redondos.
EL CILINDRO
Las columnas de un templo clásico, un rodillo de amasar o el rulo de una
apisonadora son también ejemplos de cilindros. El cilindro se forma al
girar un rectángulo alrededor de uno de sus lados, que se mantiene fijo,
como en una puerta giratoria. Los elementos del cilindro son:
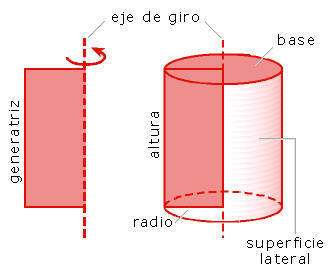 |
- Las bases: son dos círculos iguales.
- El radio del cilindro: es el radio de las bases.
- El eje: es la recta imaginaria sobre la que se encuentra el lado alrededor del cual el rectángulo gira para formar el cilindro.
- La generatriz: es el lado del rectángulo opuesto al eje de giro.
- La altura del cilindro: es la longitud de la generatriz.
- La superficie lateral: es la cara curva del cilindro.
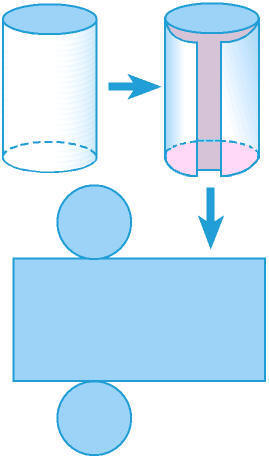
Si cortamos el cilindro
por su superficie lateral, en vertical, y por los bordes de sus bases, y
lo extendemos sobre una superficie plana, obtenemos su desarrollo:
 |
EL CONO
El cucurucho de un helado y el tejado de una choza son ejemplos de
conos. El cono se forma al girar un triángulo rectángulo alrededor de
uno de sus catetos. Los elementos del cono son:
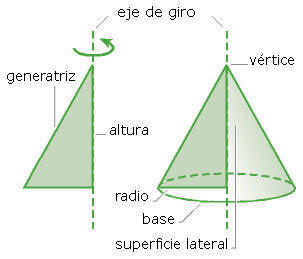 |
- La base: es el círculo sobre el que se apoya.
- El radio del cono: es el radio de la base.
- El vértice: es la cúspide o pico del cono.
- La generatriz: es la hipotenusa del triángulo rectángulo que forma el cono al girar o, lo que es lo mismo, cualquier segmento trazado entre el vértice del cono y un punto del contorno o circunferencia de su base.
- El eje: es la recta imaginaria sobre la que se encuentra el cateto sobre el que gira el triángulo rectángulo para formar el cono.
- La altura: es la longitud del cateto sobre el que gira el triángulo rectángulo.
- La superficie lateral: es la cara curva del cono.
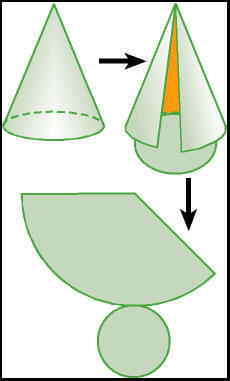
Si cortamos el cono por
su superficie lateral, siguiendo la generatriz, y por el borde de su
base, y lo extendemos sobre una superficie plana, obtenemos su
desarrollo:
 |
LA ESFERA
Una pelota de playa, una naranja o una canica son ejemplos de esferas.
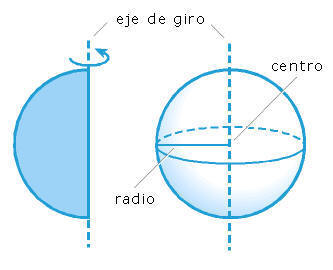
La esfera se forma por el giro de un semicírculo alrededor de su
diámetro. Los principales elementos de una esfera son su centro y
su radio.
 |
La esfera no tiene desarrollo como los demás cuerpos geométricos.
Al cortar una esfera de distintas maneras, con superficies planas, obtenemos distintas figuras: hemisferio, casquete esférico o zona esférica.
El hemisferio, si la cortamos
por la mitad.
 |
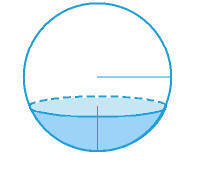
El casquete esférico,
si cortamos la esfera con una sola superficie plana y no por el centro.
En la Tierra, que es prácticamente una esfera, llamamos casquetes
polares a los situados junto al polo norte y al polo sur.
 |
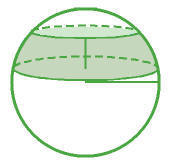
La zona esférica, si la
cortamos con dos superficies planas y paralelas.
 |
LA ESFERA TERRESTRE
Como la Tierra tiene forma casi esférica (está un poco achatada por los polos), la llamamos la esfera terrestre.
Sobre ella trazamos unas líneas imaginarias, que nos permitirán precisar
la posición de cualquier punto sobre ella, por ejemplo, la situación de
tu pueblo o ciudad. Esas líneas son: el eje terrestre, el ecuador, los
paralelos y los meridianos.
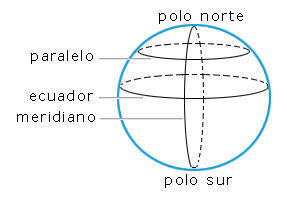 |
El eje de rotación o eje terrestre, en cuyos extremos se sitúan el polo norte y el polo sur.
El ecuador, que es la circunferencia máxima perpendicular al eje terrestre.
Los paralelos, circunferencias paralelas al ecuador, menores que él.
Los meridianos, semicircunferencias que unen los polos. Se llama meridiano cero al que pasa por Greenwich, que es una ciudad inglesa muy cerca de Londres.
www.proyectosalonhogar.com