| |
|
Las matrices son objetos matemáticos de gran utilidad en el manejo
organizado de información que puede ser suministrada en datos
numéricos. En especial, cuando están asociadas a transformaciones
lineales entre espacios vectoriales, las matrices simplifican el
estudio de sus propiedades, como se apreciará a continuación. |
Matrices Cuadradas y Matrices Rectangulares.
Una matriz es un arreglo, en filas y columnas, de números que son
llamados coeficientes. Por ejemplo, el siguiente arreglo constituye
una matriz:
|
La matriz 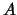 tiene dos filas:
tiene dos filas: 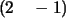 y
y  . .
Tiene dos columnas:
 y
y 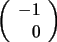
|
|
Se dice que 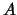 es una matriz cuadrada, porque tiene igual número de filas que de
columnas. Se dice también que
es una matriz cuadrada, porque tiene igual número de filas que de
columnas. Se dice también que 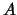 es una matriz de orden
es una matriz de orden 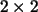 ,
lo que indica que tiene 2 filas y 2 columnas. La primera columna de ,
lo que indica que tiene 2 filas y 2 columnas. La primera columna de 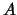 es
es  y la segunda,
y la segunda, 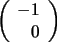 .
El orden de filas y columnas es importante. Si se cambia este orden,
cambia la matriz. Las matrices rectangulares son aquellas que tienen
diferentes números de filas y columnas. Por ejemplo, la matriz: .
El orden de filas y columnas es importante. Si se cambia este orden,
cambia la matriz. Las matrices rectangulares son aquellas que tienen
diferentes números de filas y columnas. Por ejemplo, la matriz: |
es una matriz de orden 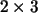 (2 filas y 3 columnas; siempre se colocan en ese orden los
números, por convención).
(2 filas y 3 columnas; siempre se colocan en ese orden los
números, por convención).
Las filas de 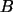 ,
que son: ,
que son: 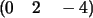 y
y 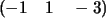 pueden considerarse como vectores en
pueden considerarse como vectores en 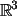 ,
y se dice que cada fila es un 'vector fila'. Igualmente, cada
columna de ,
y se dice que cada fila es un 'vector fila'. Igualmente, cada
columna de 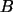 se puede considerar como un vector en
se puede considerar como un vector en 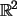 : :
 se identifica con el vector
se identifica con el vector 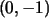 , ,
 con
con 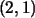 y
y 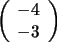 con
con 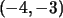 .
.
|
Cada columna es un 'vector
columna'. Cuando se quiere hacer referencia a la posición que ocupa
un coeficiente en una matriz, se nombra primero la fila y luego la
columna a las cuales pertenece el coeficiente; por ejemplo en la
matriz 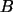 , el
coeficiente 1 está en la segunda fila, segunda columna. , el
coeficiente 1 está en la segunda fila, segunda columna.
|
|
Las transformaciones lineales
están asociadas a las matrices de la siguiente manera:
Si 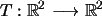 es la transformación lineal definida así:
es la transformación lineal definida así: |
Entonces su matriz asociada será:
Los coeficientes de 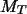 se calculan a partir de la definición de la transformación
se calculan a partir de la definición de la transformación
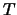 . . |
| |
Esta manera de construir la matriz 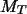 a partir de
a partir de 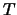 ,
permite obtener la imagen, mediante ,
permite obtener la imagen, mediante 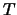 ,
de cualquier vector ,
de cualquier vector 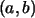 de
de 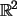 ,
haciendo las operaciones siguientes, escribiendo el vector ,
haciendo las operaciones siguientes, escribiendo el vector 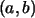 como vector columna, a la derecha de
como vector columna, a la derecha de 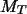 : :
|
1. Se ha multiplicado cada coeficiente de la primera fila
de 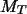 por por 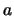 y
y 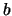 respectivamente, y se han sumado los resultados:
respectivamente, y se han sumado los resultados: |
|
|
|
Este número es la primera coordenada del vector
columna
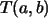 . .
2. Se hacen las mismas
operaciones con la segunda fila de 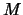 y
y 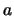 y y 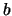 : :
|
Así, se ha obtenido la segunda coordenada del vector columna
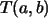 .
Finalmente, se obtiene: .
Finalmente, se obtiene:
|
Por ejemplo, al calcular 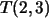 usando la definición de
usando la definición de 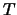 ,
se obtiene: ,
se obtiene:
|
Ahora, realizando la operación definida antes entre 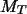 y
y 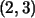 ,
se obtiene: ,
se obtiene:
|
Algunas matrices de orden 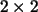 , que son importantes, son las siguientes:
, que son importantes, son las siguientes:
1. 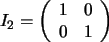 .
Esta es la matriz identidad, que corresponde a la transformación
identidad .
Esta es la matriz identidad, que corresponde a la transformación
identidad 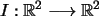 ,
definida por ,
definida por 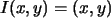 .
Si aplicamos la transformación .
Si aplicamos la transformación 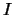 (o la matriz
(o la matriz 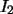 )
a los vectores del plano, éstos quedan fijos: )
a los vectores del plano, éstos quedan fijos:
|
Una figura cualquiera del plano,
quedaría fija después de aplicar la transformación 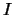 .
(Ver figura de la derecha) .
(Ver figura de la derecha) |
|
2. 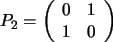 .
Esta es llamada la matriz de permutación de orden 2, pues se
obtiene a partir de la matriz identidad, intercambiando (o
permutando) las 2 columnas de .
Esta es llamada la matriz de permutación de orden 2, pues se
obtiene a partir de la matriz identidad, intercambiando (o
permutando) las 2 columnas de 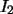 . .
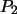 corresponde a la transformación
corresponde a la transformación 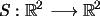 que se define como,
que se define como, 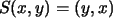 ,
y que constituye la simetría con respecto a la recta ,
y que constituye la simetría con respecto a la recta 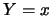 . .
|
|
El triángulo de la figura
anterior, después de aplicarle 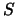 (o
(o 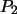 ),
se transforma en el triángulo siguiente: (Ver
figura de la izquierda) ),
se transforma en el triángulo siguiente: (Ver
figura de la izquierda) |
3. 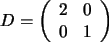 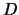 es una matriz diagonal como lo es toda matriz con ceros en todos
los coeficientes, a excepción de los de la diagonal (al menos de
algunos de ellos). Su efecto sobre el triángulo isósceles de la
figura sería: (Ver figura de la derecha)
es una matriz diagonal como lo es toda matriz con ceros en todos
los coeficientes, a excepción de los de la diagonal (al menos de
algunos de ellos). Su efecto sobre el triángulo isósceles de la
figura sería: (Ver figura de la derecha)
|
|
(Se ensancha la figura en el sentido horizontal, al doble, y en
sentido vertical, permanece igual).
|
|
4. 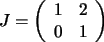 El efecto de
El efecto de 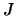 sobre el triángulo dado es el siguiente:
(Ver figura de la izquierda)
sobre el triángulo dado es el siguiente:
(Ver figura de la izquierda)
|
|
Las matrices que no son cuadradas
también se utilizan para representar transformaciones lineales, pero
no son transformaciones del plano en sí mismo, ni del espacio en sí
mismo, sino de 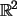 en
en 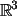 (las matrices 3x2) ó de
(las matrices 3x2) ó de 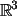 en
en 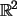 ( las matrices 2x3). Por ejemplo, la matriz siguiente:
( las matrices 2x3). Por ejemplo, la matriz siguiente:
|
Representa una trnasformación lineal de 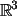 en
en 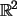 ,
y la imagen de un vector ,
y la imagen de un vector 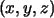 de
de 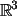 viene dada por:
viene dada por:
|
Es decir, si 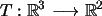 es la transformación lineal asociada a la matriz
es la transformación lineal asociada a la matriz 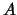 ,
entonces ,
entonces 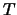 está definida así:
está definida así:
|
Se observa que 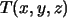 tiene 2 coordenadas, es decir, es un vector de
tiene 2 coordenadas, es decir, es un vector de 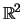 .
Por ejemplo, .
Por ejemplo,
|
Las matrices cuadradas de orden 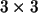 representan transformaciones lineales de
representan transformaciones lineales de 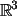 en
en 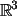 . .
Por ejemplo, si
|
Puede aplicarse 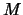 a cualquier vector
a cualquier vector 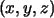 en
en 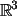 y se obtiene un vector columna de tres filas, es decir, otro
vector en
y se obtiene un vector columna de tres filas, es decir, otro
vector en 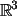 . .
Por ejemplo,
|
El determinante de una matriz
cuadrada 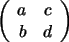 es el número real que se obtiene al efectuar las operaciones:
es el número real que se obtiene al efectuar las operaciones: |
Se usa la notación siguiente:
|
Por ejemplo, si 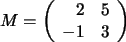 entonces el determinante de
entonces el determinante de 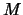 ,
que se denota por ,
que se denota por 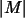 ,
es: ,
es:
|
El signo (positivo o negativo) del determinante de una matriz 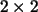 tiene un significado geométrico; se explicará a través del ejemplo
anterior.
tiene un significado geométrico; se explicará a través del ejemplo
anterior.
|
Los vectores columna de 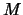 son:
son:
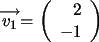 y
y 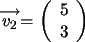 . .
|
Se representan 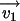 y
y 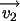 en el plano cartesiano: (Ver figura de la
derecha)
en el plano cartesiano: (Ver figura de la
derecha)
|
|
El ángulo que forman 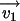 y
y 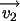 ,
medido a partir de ,
medido a partir de 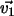 y en sentido opuesto a las agujas del reloj, es menor que
y en sentido opuesto a las agujas del reloj, es menor que 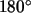 y mayor que
y mayor que 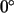 .
Se puede demostrar que, por eso, el determinante de .
Se puede demostrar que, por eso, el determinante de 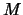 (matriz formada por los vectores columna
(matriz formada por los vectores columna 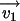 y
y 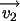 )
es positivo. Así, cada vez que eso ocurra, es decir, cuando el
ángulo entre los vectores columna, medido a partir del primer vector
en el sentido indicado, sea menor que )
es positivo. Así, cada vez que eso ocurra, es decir, cuando el
ángulo entre los vectores columna, medido a partir del primer vector
en el sentido indicado, sea menor que 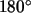 y mayor que
y mayor que 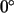 ,
el determinante será positivo. ,
el determinante será positivo. |
|
|
Cuando el ángulo 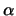 formado por
formado por 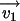 y
y 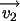 es mayor que
es mayor que 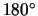 y menor que
y menor que 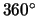 ,
el determinante es negativo. Por ejemplo: (Ver
figura de la izquierda) ,
el determinante es negativo. Por ejemplo: (Ver
figura de la izquierda)
|
Cuando el ángulo 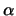 formado por
formado por 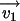 y
y 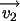 es igual a
es igual a 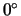 ó
ó 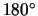 ,
entonces ,
entonces 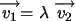 ,
para algún número real ,
para algún número real 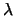 ,
es decir, ,
es decir, 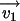 y
y 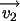 son linealmente dependientes y geométricamente, están sobre la
misma recta; por ejemplo: (Ver figura de la
derecha)
son linealmente dependientes y geométricamente, están sobre la
misma recta; por ejemplo: (Ver figura de la
derecha)
|
|
En este caso, el ángulo que forman 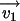 y
y 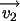 es igual a cero y el determinante también es cero:
es igual a cero y el determinante también es cero:
Así, en general, siempre que dos vectores del
plano sean linealmente dependientes, el determinante de la matriz 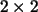 que ellos forman -como vectores columna- es nulo:
que ellos forman -como vectores columna- es nulo:
Si 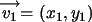 y
y 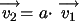 ,
es decir, ,
es decir, 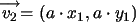 ,
entonces ,
entonces
|
|
|
Hay otra interpretación geométrica del determinante de una matriz
cuadrada 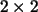 : :
El valor absoluto del determinante de la matriz
Es igual al área del paralelogramo que tiene
como lados a los vectores 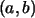 y
y 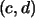 ,
y al vector ,
y al vector 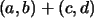 como diagonal: (Ver figura de la izquierda)
como diagonal: (Ver figura de la izquierda)
|
En efecto, para calcular el área
del paralelogramo anterior, se puede hacer lo siguiente:Se calcula
el área del triángulo 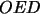 y se le suma al área del trapecio
y se le suma al área del trapecio 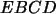 . .
A esa área se le restan luego el área del triángulo
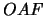 y el área
del trapecio y el área
del trapecio 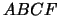 .
areas y Volumenes .
areas y Volumenes
Es decir: área 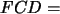 área
área 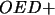
área 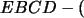 área área
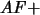 área área
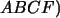
|
|
Tomando en cuenta las coordenadas de los puntos 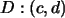 , ,
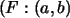 y
y 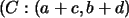 ,
se tiene: ,
se tiene:
|
área
|
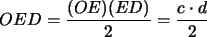 |
|
área |
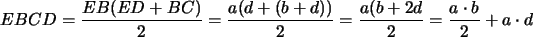 |
|
área |
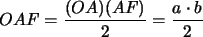 |
|
área |
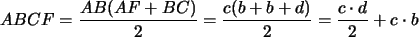 |
|
Por lo tanto, área |
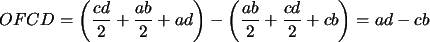 |
|
y precisamente, |
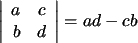 |
|
| |
Como los vectores 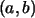 y
y 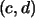 fueron escogidos de manera tal que el ángulo formado entre ellos,
medido a partir de
fueron escogidos de manera tal que el ángulo formado entre ellos,
medido a partir de 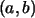 y en sentido contrario a las agujas del reloj, fuese mayor que
cero y menor que
y en sentido contrario a las agujas del reloj, fuese mayor que
cero y menor que 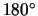 ,
resulta que el determinante es positivo y coincide con su valor
absoluto. Es fácil ver que, cuando el ángulo formado por estos
vectores es mayor que ,
resulta que el determinante es positivo y coincide con su valor
absoluto. Es fácil ver que, cuando el ángulo formado por estos
vectores es mayor que 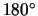 ,
el área del paralelogramo tiene el signo opuesto al del
determinante. ,
el área del paralelogramo tiene el signo opuesto al del
determinante.
La interpretación del valor absoluto del determinante como el área
del paralelogramo formado por los vectores columna, también permite
interpretar el hecho de que el determinante de una matriz cuyos
vectores columna son linealmente dependientes sea nulo: el área del
paralelogramo en cuestión, en este caso también sería nula, pues dos
vectores linealmente dpendientes son colineales y no generan
un paralelogramo sino un segmento de recta.
El determinante de una matriz 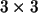 se calcula de la siguiente manera:
se calcula de la siguiente manera:
|
Se observa que cada sumando en la expresión anterior es igual al
producto de 3 coeficientes. En la siguiente figura se trazarán
líneas que conectan con azul los productos que llevan signo
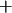 y con rojo los que llevan signo
y con rojo los que llevan signo  : : |
Propiedades del Determinante. El determinante de una
matriz cuadrada tiene ciertas propiedades que es muy importante
conocer:
1. Cuando se intercambian filas o columnas
de una matriz, el determinante de la matriz cambia de signo.
Ejemplos:
|
2.Cuando dos filas o dos columnas son
iguales, el determinante es igual a cero: Ejemplo:
|
3. Cuando una fila (o columna) es combinación lineal de otra(s),
el determinante es igual a cero. En el siguiente ejemplo, la
tercera columna es igual a la suma de la primera más el doble de
la segunda:
|
4. Si en una matriz  se multiplica una columna o una fila por un número real
se multiplica una columna o una fila por un número real
 ,
entonces el determinante de la matriz resultante es igual a ,
entonces el determinante de la matriz resultante es igual a 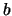 por el determinante de
por el determinante de 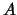 :
Dada A (ver tabla inferior) y se
multiplica la primera columna de :
Dada A (ver tabla inferior) y se
multiplica la primera columna de 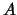 por 2, se obtiene:
por 2, se obtiene:
|
El determinante de 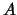 es:
es:
|
y por otra parte,
|
5. Si 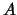 es
una matriz cuadrada y es
una matriz cuadrada y 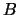 es otra matriz que tiene todas sus columnas (o filas) iguales a
las de
es otra matriz que tiene todas sus columnas (o filas) iguales a
las de 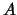 ,
excepto por una de ellas, y esta última columna de ,
excepto por una de ellas, y esta última columna de 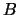 es igual a la suma de la columna correspondiente de
es igual a la suma de la columna correspondiente de 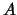 más una combinación lineal de las demás, entonces
más una combinación lineal de las demás, entonces 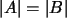 .
Por ejemplo, si .
Por ejemplo, si
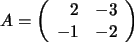 |
y
|
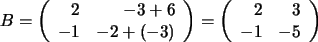 |
|
(la segunda columna de 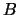 es igual a la suma de la segunda columna de
es igual a la suma de la segunda columna de 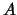 más el triple de la primera) entonces
más el triple de la primera) entonces
|
En efecto:
|
|
|
|
|
Fundación
Educativa Héctor A. García |