| |
| |

MODELOS
LINEALES
|
Para poder tomar los
exámenes
de este tema debes
estar
registrado, si no
lo estás,
Registrate
aquí
Entrar a exámenes de:
Contenido Revisado 
|
|
|

Funciones y
dominios
Una
función real f de una variable
es una regla que asigna a cada número real
x en un conjunto especificado de
números reales llamado el dominio de
f, un número real único
f(x).
La variable
x se llama la
variable independiente. Si y =
f(x)
llamamos a y la
variable dependiente.
Una función puede ser
especificado:
-
numéricamente:
por medio de una tabla
-
algebráicamente:
por medio de una formula
-
gráficamente:
por medio de una gráfica.
Nota
acerca de los dominios
El dominio de una función no es siempre explícitamente
especificado; cuando no se especifica algún dominio para una
función f, supondremos que el
dominio está el conjunto más grande de los números
x para los cuales tiene sentido
f(x).
Esta "dominio más grande posible" se le llama a veces el
dominio natural.
Pulse aquí para ir a una
página que se deja evaluar y dibujar a las curvas de
funciones.
Pulse aqui para descargar una
graficador Excel.
Regresar |

Ejemplos
Función especificado numéricamente
Sea f la función
especificada por la siguiente tabla:
|
x |
0 |
1 |
2 |
3 |
|
f(x)
|
3.01 |
-1.03 |
2.22 |
0.01 |
Entonces,
f(0) = 3.01, f(1)
= -1.03, y así sucesivamente.
Función especificado algebráicamente:
Sea f
la función especificada por f(x)
= 3x2 - 4x
+ 1. Entonces
f(2)
= 3(2)2 - 4(2) + 1 = 12 - 8 + 1 = 5,
f(-1) = 3(-1)2 -
4(-1) + 1 = 3 + 4 + 1 = 8.
Como f(x)
se defina para toda x, el dominio
de f es el conjunto de todos
números reales.
Función especificado gráficamente:
Sea f la función
especificada por la siguiente gráfica.

Entonces,
f(0) = 1, f(1)
= 0, y f(3) = 5.
Regresar |
|
Intervalos
El
intervalo cerrado [a, b] es el
conjunto de todos números reales x
tal que a ≤ x
≤ b.
El
intervalo abierto (a, b) es el
conjunto de todos números reales x
tal que a < x
< b.
El intervalo (a,
∞) es el conjunto de todos números reales
x tal que a <
x < +∞, y (-∞,
b) es el conjunto de todos números reales
x tal que -∞ <
x < b.
Tenemos tembién
intervalos medios abiertos de la forma
[a, b) y (a, b].
Regresar |
Ejemplos
|
Intervalo |
Dibujo |
Descripción |
|
[-1, 6) |
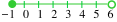 |
-1
≤ x < 6 |
| (2,
4) |
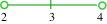 |
2 <
x < 4 |
|
(-∞, 0] |
 |
-∞
< x ≤ 0 |
Regresar |
|
Gráfica de una función
La gráfica
de una función f es el conjunto de
todos puntos (x,
f(x)) en
el plano-xy, tal que restringimos
los valores de x al estar en el
dominio de f.
La siguiente diagrama
muestra la gráfica de una función:

Prueba de la recta vertical
Para que una gráfica sea la gráfica de una función, cada
recta vertical debe intersecarse con la gráfica en un solo
punto.
Regresar |
Ejemplo
Para obtener la gráfica de
-
f(x)
= 3x2 - 4x
+ 1
Forma de función
con dominio restringido a [0,
+ ∞), sustituimos f(x)
por y, y obtenemos la ecuación
-
y
= 3x2 - 4x
+ 1. Forma de ecuación
Entonces obtenemos la gráfica
por trazando puntos, donde restringimos a
x al estar en [0, + ∞), y obtenemos el siguiente
dibujo:

No hay nada a la izquierda
del eje-y, pues hemos restringido
a x al estar ≥ 0.
Regresar |
|
Funciones lineales
Una
función lineal es una función de la forma
|
f(x)
= mx +
b |
|
Notación de función |
|
y =
mx +
b |
|
Notación de ecuación |
donde m
y b son números fijos (los nombres
'm' y 'b'
son tradicionales).
Papel de m:
Si y =
mx + b,
entonces:
(a) y cambia
en m unidades para cada cambio de
x en una unidad.
(b) Un
cambio de Δx unidades en
x resulta en un cambio de Δy
= mΔx
unidades en y.
(c) Despejando a m,
se obtiene
| m |
= |
Δy

Δx
|
= |
Cambio en y

Cambio en
x
|
Papel de b:
Cuando x = 0,
y = b
(forma de ecuación), o f(0) =
b (forma de función)
Regresar |
Ejemplos
La función
-
f(x)
= 5x - 1
es una función lineal donde
m = 5 y b
= -1.
Las siguientes ecuaciones
se puede solucionar para y como
funciones lineales de x.
| 3x
- y + 4 = 0 |
|
y
= 3x + 4 |
| 4y
= 0 |
|
y = 0 |
| 3x
+ 4y = 5 |
|
y
= -(3/4)x + 5/4 |
Regresar |
|
Rectas
La gráfica de una ecuación
lineal es una recta. El pendiente de la
recta que pasa por (x1,
y1) y (x2,
y2) es se expresa por
la formula
| m |
= |
y2
- y1

x2 -
x1
|
= |
Δy

Δx
|
La gráfica de la función
lineal
| |
f(x)
= mx +
b |
|
Forma de función |
| o |
| |
y =
mx + b
|
|
Forma de ecuación |
es una recta con pendiente
m y intersección en
y igual a b.
Regresar |
Ejemplos
El pendiente de la recta
que pasa por (2, -3) y (1, 2) se expresa por
| m |
= |
y2
- y1

x2 -
x1
|
| |
= |
2 + 3

1 - 2 |
| |
= |
-5. |
Para ver como dibujar la
gráfica de una función lineal, vea el siguiente tópico.
Regresar |
|
Dibujando la gráfica de una
función lineal
Hay dos métodos buenos para
dibujar la gráfica de una función lineal.
(a)
Escriba la función en la forma y =
mx+b, y
después dibuje la recta con intersección en
y igual a b
y pendiente igual a m.
(b)
Calcule las intersecciones en x y
y, y después dibuje la recta que
pasa por aquellos dos puntos. Para calcular la intersección
en x de una recta, establezca
y = 0 en su ecuación y despeje a
x. Para calcular la intersección
en y, establezca
x = 0, y despeje a
y. Este método sirva solo cuando
la recta no pasa por el origen. En este caso, tendrá que
trazar un punto adicional o usar el primero método.
|
Ejemplos
Aquí son estas técnicas
aplicadas a la recta con ecuación 2x
- 3y = -6.
(a)
Despejando a y, obtenemos
y = 2x/3
+ 2. Entonces, el pendiente es 2/3 y la intersección en
y es 2. La siguiente figura
muestra dos pasos para dibujar la gráfica.
Paso 1
Empiece con la intersección en y. |
Paso 2
Dibuje una recta con la pendiente que se da.
|
Intersección-y
=2
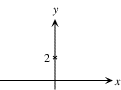 |
Pendiente = 2/3
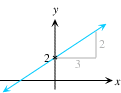 |
(b) Para obtener la intersección en
x, establezca y
= 0. La ecuación se convierte a 2x
- 3(0) = -6 y obtenemos x = -3.
Esta es la intersección en x. Para
obtener la intersección en y,
establezca x = 0, y obtenemos 2(0)
- 3y = -6, entonces
y = 2. La siguiente figura muestra
dos pasos para dibujar la gráfica.
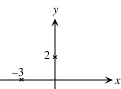
Paso 1
Empiece con las intersecciones en
x y en y.
Intersección-x = -3
Intersección-y = 2
|
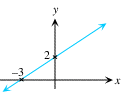
Paso 2
Dibuje la recta que pasa por las dos intersecciones.
|
 |
 |
Regresar |
|
Ajustando una ecuación lineal
a datos: Como hacer un modelo lineal
Formula punto-pendiente:
Una ecuación de la recta
que pasa por el punto (x1,
y1) con pendiente
m es
| |
y =
mx + b
|
|
| donde |
| |
b
= y1 -
mx1
|
Cuando
aplicar la formula punto-pendiente
- Aplique la formula
punto-pendiente para determinar la ecuación de una recta
siempre que tiene información acerca un punto y la
pendiente de la recta. La formula no se aplica si la
pendiente es indefinida.
- Si ya sabe la
pendiente m y la intersección
b en y,
entonces puede sencillamente escribir la función lineal
como
y = mx
+ b.
Esta formula se llama la
formula pendiente-intersección.
Rectas verticales y horizontales
Una ecuación de la recta
horizontal que pasa por (x1,
y1) es
-
y =
y1.
Una ecuación de la recta
vertical que pasa por (x1,
y1) es
-
x =
x1.
Regresar |
Ejemplos
Una ecuación de la recta
que pasa por (1, 2) con pendiente -5 es
| |
y
= -5x +
b, |
| donde |
| |
b
= y1 -
mx1 = 2 -
(-5)(1) = 7 |
| entonces |
| |
y
= -5x + 7. |
Una ecuación de la recta
horizontal que pasa por (3, -4) es
Una ecuación de la recta
vertical que pasa por (3, -4) es
Regresar |
|
Interpretación de la pendiente
en aplicaciones
La pendiente de la recta
y = mx +
b es la razón de cambio de
y para cada cambio de
x en una unidad. Las unidades de
medida de la pendiente son unidades de
y por unidad de
x
Si y
es desplazamiento y x es tiempo,
entonces la pendiente representa la
velocidad. Sus unidades son unidades de medida de
desplazamiento por unidad de tiempo (por ejemplo, metros por
segundo).
Si y
es costo y x es el número de
artículos, entonces la pendiente representa
costo marginal. Sus unidades son unidades de costo por
artículo (por ejemplo, euros por artículo).
Regresar |
Ejemplo
El número de páginas web en
este sitio se puede expresar por la ecuación
-
n = 1.2t
+ 200,
donde t
es tiempo en semanas desde 1 de junio, 1997. La pendiente es
m = 1.2 páginas web por semana.
Entonces, el número de páginas está creciendo a una tasa de
1.2 páginas por semana.
Regresar |
|
Costo, ingreso y utilidad
Una
función (de) costo C
especifica el costo C(x)
como una función del número de artículos
x.. Una función costo lineal
tiene la forma
-
C(x)
= mx + b,
donde m
es el costo marginal, y
b es el costo
fijo. Una función ingreso
R especifica el ingreso
R(x) que
resulta de la venta de x
artículos. Una función utilidad
P especifica la utilidad
(ingreso neto) P(x)
que resulta de la venta de x
artículos. Las funciones costo, ingreso y utilidad se
relacionan con la formula
-
P(x)
= R(x)
- C(x).
Equilibrio se ocurre cuando
-
P(x)
= 0
o, equivalentemente, cuando
-
R(x)
= C(x).
Regresar |
Ejemplo
Si el costo fijo es $400, y
si el costo marginal es $40 por artículo, y si se vende los
artículos a $60 cada uno, entonces
C(x)
= 40x + 400
R(x)
= 60x
P(x)
= R(x)
- C(x)
= 60x - (40x
+ 400)
= 20x - 400.
Para equilibrio,
entonces x
= 20. Por lo tanto, tiene que vender 20 artículos para
alcanzar el equilibrio.
Regresar |
|
Demanda y ingreso
Una
función lineal (de) demanda tiene la forma
q = mp + b,
donde q es la demanda (número de
artículos vendidos) y p es el
precio por artículo. Se puede construir una ecuación demanda
lineal a saber la demanda a dos precios distintos. El
ingreso que resulta es
-
R = pq
(Precio por cantidad).
Se puede especificar
ingreso como una función de p solo
si se usa la ecuación demanda para sustituye por
q. |
Ejemplo
Si se vende 100 camisetas
por semana cuando el precio es $10, y 200 por semana cuando
se baja el precio hasta $8, entonces la ecuación (lineal)
demanda es
q
= -50p + 600
Ecuación de recta por (10, 100) y (8,
200)
Entonces, la función ingreso
relacionada es
R
= pq = p(-50p+600)
= -50p2 + 600p.
Regresar
|
|
Regresión lineal
Valores observados y pronosticados
Supongamos que tenemos un
conjunto de puntos de datos (x1,
y1), ..., (xn,
yn).
Las n cantidades
y1,
y2, ..., yn
se llaman los valores observados
y. Si se modela estos datos
con una ecuación lineal

y
|
= |
mx
+ b |
|

y |
representa y
"estimada" o "pronosticada". |
entonces los valores de
y que se obtiene por sustituir
x en la ecuación por los valores
dados de x se llaman los
valores y
pronosticados:

y1
|
= |
mx1
+ b |
|
Sustituya x por
x1 |

y2
|
= |
mx2
+ b |
|
Sustituya x por
x2
|
| . . .
|

yn
|
= |
mxn
+ b |
|
Sustituya x por
xn
|
Residuos y error suma de cuadrados, (SSE)
Si modelamos un conjunto de
datos (x1,
y1), ... , (xn,
yn)
con una ecuación lineal como más arriba, entonces los
residuos son los n
cantidades (Valor actual - valor pronosticado):

(y1 -
y1), |

(y2 -
y2), |
. . . , |

(yn
- yn) |
El error
suma de cuadrados (SSE) es la suma de cuadrados de los
residuos:
|
SSE = |

(y1 -
y1)2
+ |

(y2 -
y2)2
+ |
. . . + |

(yn
- yn)2
+ |
Recta de
regresión
La recta
de regreión (recta de mínimos
cuadrados, recta de mejor ajuste) relacionada con los
puntos (x1,
y1), (x2,
y2), . . ., (xn,
yn)
es la recta que se minimiza el valor de SSE.
La recta de regresión se
representa por
donde
| m |
= |
n(Σxy)
- (Σx)(Σy)

n(Σx2)
- (Σx)2
|
| b |
= |
Σy
- m(Σx)

n
|
| n |
= |
número de
puntos de datos |
Regresar |
Ejemplos
Valores observados y pronosticados
Para los tres puntos de
datos (0, 2), (2, 5), y (4, 6), los valores observados de
y son y1
= 2, y2 = 5, y
y3 = 6. Si modelamos
estos datos con la ecuación

y
|
= |
2x
+ 1.5 |
entonces los valores
pronosticados se obtiene por sustituir x
en la ecuación de la recta por los valores dados de
x:
Residuos y error suma de cuadrados, (SSE)
Para los tres puntos de
datos (0, 2), (2, 5), y (4, 6) y el modelo lineal 2x
+ 1.5 que se muestra más arriba, los residuos son:
El error suma de cuadrados
se obtiene por cuadrar y sumar las respuestas:
SSE = (0.5)2 +
(-0.5)2 + (-3.5)2 = 12.75
Regresar |
RegresarFundación Educativa
Héctor A. García
|
|
|
|
|
|