
La Multiplicación
|

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
Registrate
aquí
Entrar a exámenes
de:
Contenido Revisado 
|
|
|
 |
La multiplicación es una
operación matemática, de aritmética
elemental, que consiste en sumar varias veces un mismo número.
La multiplicación es una
suma abreviada de
sumandos iguales, que pueden repetirse muchas veces.
Por ejemplo, según esto,
5 x 2 significa
5 veces el 2.
|
Entonces:
|
5
x 2
=
2 +
2 + 2
+ 2
+ 2
=
10
|
| |
|
|
|
|
5 veces
|
|
|
|
|
Podemos graficarlo a través de conjuntos.
Utilizaremos estrellas.
5 conjuntos de 2 estrellas
= 10 estrellas
-----> 5
x 2 =
10
También se puede relacionar la multiplicación con
los pares ordenados, que se obtienen del producto cartesiano de 2
conjuntos.
Los pares se forman con un elemento de cada
conjunto, en el orden que se dan.
Cómo
Aprender
 |
Tu vida será mucho más fácil
cuando puedas simplemente recordar las tablas de
multiplicar. Así que... ¡entrena tu memoria!
Primero, usa la tabla que te incluimos en este enlace [ver
tablas] para empezar a aprender las respuestas y para
entrenar la memoria, está especialmente diseñado para ayudar a
memorizar las tablas. Úsalo varias veces al día durante cinco
minutos cada vez, y aprenderás las tablas. |
| |
Entonces, las dos maneras principales
de aprender las tablas de multiplicar son:
- Leer la tabla
- Practicar varias veces al día por
(5) cinco minutos.
Pero aquí tienes algunos "consejos"
especiales para ayudarte todavía más:
Consejo 1: El Orden no Importa
Cuando
multiplicas dos números, no importa cuál es el primero y
cuál es el segundo, la respuesta es la misma.
|
Ejemplo: 3×5=15, y 5×3=15
Otro ejemplo: 3×9=27, y 9×3=27
|
De hecho, ¡la mitad de la tabla es como un reflejo en un
espejo de la otra mitad!
Así que no memorices ambos
"3×5" y "5×3", aprende sólo que "un 3 y un 5 dan 15" al
multiplicarlos.
¡Esto es muy importante!
La cantidad de trabajo se queda en la mitad. |
|
 |
|
En tu mente deberías tener la
idea de que
3 y 5 "juntos" hacen 15.
así que deberías pensar algo
como esto: |
|
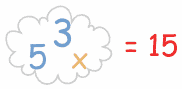 |
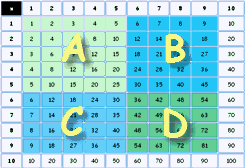
Consejo 2: Aprende las Tablas "a
trozos"
Es muy difícil aprender toda la tabla
de golpe. Así que apréndela "a trozos"...
 |
| |
A |
|
Empieza por aprender
la tabla del cinco. |
| |
B |
|
Después aprende hasta
nueve por cinco. |
| |
C |
|
Igual que B,
pero las preguntas al revés. Apréndelas también. |
| |
D |
|
Finalmente aprende el
trozo desde 6×6 a 9×9 |
| |
|
|
|
| |
Y júntalo todo practicando
la "Tabla del diez" completa |
|
¡Y ya te has aprendido
la Tabla del diez!
(Miremos la tabla del
doce que está debajo)
|
|
|
- |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
3 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
33 |
36 |
|
4 |
0 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
|
5 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
6 |
0 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
72 |
|
7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
77 |
84 |
|
8 |
0 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
88 |
96 |
|
9 |
0 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
99 |
108 |
|
10 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
|
11 |
0 |
11 |
22 |
33 |
44 |
55 |
66 |
77 |
88 |
99 |
110 |
121 |
132 |
|
12 |
0 |
12 |
24 |
36 |
48 |
60 |
72 |
84 |
96 |
108 |
120 |
132 |
144 |
|
|
|
Tabla pitagórica del (12)
doce
Algunas pautas/Algunos patrones
Hay algunas pautas que pueden ayudarte
a recordar:
2×
es simplemente doblar el número. Lo mismo que sumar el número a sí mismo.
dos veces el dos = (2×2=4),
dos veces el tres = (2×3=6),
o dos veces el cuatro (2×4=8)
y así etc...
Así que la pauta es
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
(Y cuando recuerdes
éstos, también sabrás 3×2, 4×2, 5×2, etc., ¿verdad?)
5×
tiene una pauta: 5, 10, 15, 20, etc. Siempre termina en cero o cinco.
10×
es quizás la más sencilla de todas... sólo pon un cero después
10×2=20, 10×3=30, 10×4=40,
etc.
9×
también sigue una pauta: 9, 18, 27, 36, 45,
54, 63, 72, 81, 90
¿Ves cómo la cifra
de las "unidades" baja: 9,8,7,6,...? ¿Y al mismo tiempo, la de las "decenas"
sube: 1,2,3,...?
Puedes usar esta
pauta para impulsar a tu memoria de esta manera: ¡la cifra de las
decenas es uno menos que el número que estás multiplicando!
Ejemplo: 9×7...
resta 1 al 7, así que la cifra de las decenas es 6, y
entonces recuerda 63
¿Y la Tabla del doce?
Suena difícil, pero cuando tengas la
tabla del 10× dominada, sólo es ir unos pasos más allá.
 |
Primero, 11× es muy fácil:
desde 11×2 hasta 11×9 sólo pones las dos cifras juntas. 11×2=22,
11×3=33, ..., 11×9=99. |
| |
|
 |
Y claro, 2×, 5× y 10× siguen
las reglas sencillas que ya conoces, así que sólo tienes que
aprenderte éstas:
- 3×12=36,
- 4×12=48,
- 6×12=72,
- 7×12=84,
- 8×12=96,
- 9×12=108
|
| |
|
 |
Y el "Gran Trío":
- 11×11=121,
- 11×12=132 y
- 12×12=144
|
Trucos
y consejos para multiplicar
Algunos trucos y consejos
Aquí tienes unos trucos que pueden
ayudarte a recordar tus tablas de multiplicar. Cada persona piensa de
una manera diferente, así que olvida los trucos que no te funcionen.
 |
Cada respuesta tiene un
gemelo, que puede ser más fácil de recordar. Por ejemplo si te
olvidas de 8×5, puedes acordarte de 5×8. Así sólo tienes que
aprenderte la mitad de la tabla. |
|
para multiplicar por
|
truco |
|
2
|
suma el número
a sí mismo (ejemplo 2×9 = 9+9) |
|
5
|
Las últimas
cifras son siempre 5,0,5,0,.., |
|
|
es siempre la
mitad de 10× (ejemplo: 5x6 = mitad de 10x6 = mitad de 60 =
30) |
|
|
es la mitad
del número multiplicado por 10 (ejemplo: 5x6 = 10x3 = 30) |
|
6
|
si multiplicas
6 por un número par, acaba en la misma cifra. Ejemplo: 6×2=12,
6×4=24, 6×6=36, etc |
|
9
|
es 10× el
número menos el número. Ejemplo: 9×6 = 10×6 - 6
= 60-6 = 54 |
|
|
La última
cifra va así: 9,8,7,6, .. |
|
|
si sumas
las cifras de la respuesta, sale 9. Ejemplo: 9×5=45 y 4+5=9.
(Pero no con 9×11=99) |
|
10
|
pon un cero
después del número |
|
11
|
hasta 9x11:
sólo repite la cifra (ejemplo: 4x11 = 44) |
| |
de 10x11 a
18x11: escribe la suma de las cifras en medio del número (ejemplo:
15x11 = 1(1+5)5 = 165)
Nota: esto funciona para todos los números de dos cifras,
pero si la suma es más de 9, tendrás que "llevarte el uno" (ejemplo:
75x11 = 7(7+5)5 = 7(12)5 = 825). |
|
12
|
es 10× más 2× |
Recordar los cuadrados puede ayudar
Quizás esto no te ayude, pero a mí sí
me ayudó. Me va bien recordar los cuadrados (cuando multiplicas un
número por sí mismo):
| 1×1=1 |
2×2=4 |
3×3=9 |
4×4=16 |
5×5=25 |
6×6=36 |
| |
|
|
|
|
|
| 7×7=49 |
8×8=64 |
9×9=81 |
10×10=100 |
11×11=121 |
12×12=144 |
Y esto vale para otro truco. Si los
números que multiplicas se diferencian en 2 (por ejemplo 7 y 5), sólo
tienes que multiplicar el número del medio por sí mismo y restar uno.
Mira:
| 5×5 = 25 es
sólo uno más que 6×4 = 24 |
| 6×6 = 36 es
sólo uno más que 7×5 = 35 |
| 7×7 = 49 es
sólo uno más que 8×6 = 48 |
| 8×8 = 64 es
sólo uno más que 9×7 = 63 |
| etc ... |
Multiplicar
mediante suma repetida
El resultado de la multiplicación es el
número total (producto) que se obtiene al combinar varios (multiplicador)
grupos de tamaño similar (multiplicando). El mismo resultado se
puede obtener por suma repetida. Si estamos combinado 7 grupos con 4
objetos en cada grupo, podríamos llegar al mismo resultado mediante
la suma. Por ejemplo, 4+4+4+4+4+4+4+= 28 es equivalente a la
ecaución multiplicativa 7 x 4= 28.
Multiplicar números de dos dígitos por números de un dígito
Como multiplicar un número de dos dígitos
por un número de un dígito.
(por ejemplo 43 x 2).
- Coloca un número sobre el otro de tal
manera que los dígitos de las unidades queden alienados. Traza
una línea debajo del número inferior.
- Multiplica los dígitos de las unidades
(3 x 2 = 6). Coloca el seis debajo de la línea en la columna de
las unidades.
- MMultiplica el dígito en la columna de
las decenas (4) por e dígito en la columna de las unidades del
segundo número (2). El resultado es 4 x 2 = 8. Coloca el
resultado debajo de la línea a la izquierda del 6.
Multiplicar números de un dígito por números de tres dígitos
Como multiplicar un número de tres dígitos
por un número de un dígito.
es decir 312 * 3)
- Coloca un número sobre el otro de tal
manera que los dígitos de las unidades queden alineados. Traza
una línea debajo del número inferior.
- Multiplica los dos dígitos de las
unidades (2 * 3 = 6). Coloca el seis debajo de la línea en la
columna de las unidades.
- Multiplica el dígito en la columna de
las decenas (1) por el dígito en la columna de las unidades del
segundo número (3). El resultado es 1 * 3: 3. Coloca el
resultado debajo de la línea a la izquierda del 6.
- Multiplica el dígito en la columna de
las centenas (3) por el segundo número (3). El resultado 3 * 3 =
9. Coloca el 9 debajo de la línea en la columna de las centenas.
Multiplicar números de dos y tres
dígitos
Como multiplicar un número de tres dígitos
por un número de dos dígitos ( es decir 529 x 67).
- Coloca un número sobre el otro de tal
manera que las centenas, las decenas y las unidades queden
alineadas. Traza una línea debajo del número inferior.
- Multiplica los dos números
correspondientes a las unidades (9 x 7 = 63). Este núemro es más
grande que 9 entonces coloca el 6 sobre la columna de las
decenas y coloca el 3 debajo de la línea en la columna de las
unidades.
- Multiplica el dígito correspondiente a
las decenas del número superior (2) por el dígito
correspondiente a las unidades del número inferior (7). La
respuesta (2 x 7=14) se suma al 6 colocado sobre la columna de
las decenas para así obtener un resultado de 20. El 0 del 20 se
coloca debajo de la línea y el 2 del 20 se coloca sobre la
columna de las centenas.
- El número correspondiente a las
centenas de la cifra superior (5) se multiplica por la unidad
del multiplicador (5 x 7=35). El dos que nos habíamos llevado a
la columna de las centenas se suma y el 37 se coloca debajo de
la línea.
- Después que el 529 se multiplicó por 7,
como mostramos anteriormente, 529 se multiplica por el número
correspondiente a la decena del multiplicador que es el 6. El
número se corre un lugar hacia la izquierda porque estamos
multiplicando por un número correspondiente a la decena. El
resultado sería 3174:
- Se traza una línea debajo del producto
inferior (3174) y se suman los productos en forma conjunta para
obtener el resultado final de 35443.
15
529
67
3703
3174
35443 |
|
|
Multiplicación de números de cinco dígitos.
A continuación se muestra como multiplicar
un número de cinco dígitos por un número de un dígito.
- Coloca una número sobre el otro de tal
manera que las unidades queden alineadas. Traza una línea debajo
del número inferior.
VER
 Multiplicación
por numeros naturales
Multiplicación
por numeros naturales

Elementos
En la multiplicación encontramos los siguientes
elementos:
| |
2 |
X |
5 |
=10 |
| |
Factor |
|
Factor |
Producto |
Así, 3 x 4, indica que tenemos que sumar 3, 4 veces,
es decir, 3 + 3 + 3 + 3. Por tanto, la
multiplicación se puede considerar como una suma
repetida.
Comprobamos que el resultado es el mismo: 3 x 4 =
12 y 3 + 3 + 3 + 3 = 12
Los términos de la
multiplicación se llaman factores y
el resultado de la misma se llama producto.
Cuando la multiplicación tiene sólo dos factores,
llamamos multiplicando al número
que vamos a sumar y multiplicador a
las veces que lo vamos a sumar.
En nuestro ejemplo el multiplicando es 3, el
multiplicador es 4, y el producto es 12, que es el
resultado de sumar 3 + 3 + 3 + 3 o multiplicar
3 x 4
Para multiplicar dos números de varias
cifras colocamos el multiplicando y
debajo el multiplicador, trazando una
raya por debajo de ambos.
Comenzamos a multiplicar, de derecha a
izquierda, la primera cifra del
multiplicador por cada una de las cifras del
multiplicando y vamos colocando las unidades de cada
producto debajo de la raya, también de derecha a
izquierda, y las decenas se las sumamos al siguiente
producto. (Como verás en el ejemplo, el primer
producto es 6 x 3 = 18, colocamos el 8 y nos
llevamos una que se la sumamos al siguiente producto
3 x 5 = 15 + 1 = 16).
Después, hacemos lo mismo con cada una
de las restantes cifras del multiplicador (decenas,
centenas ...) y las vamos colocando debajo de la
fila anterior, desplazadas un lugar
a la izquierda.
Cuando terminemos de multiplicar la última
cifra del multiplicador por todas
las del multiplicando, trazamos una raya debajo de
la última fila (tendremos tantas filas como cifras
tenga el multiplicador) y procederemos a
sumar ordenadamente todas las filas. El
resultado obtenido será el producto
de la multiplicación.
Veamos otro
ejemplo:
| |
|
|
|
3 |
2 |
5 |
6 |
| |
|
|
|
x |
4 |
2 |
3 |
| |
|
|
___ |
___ |
___ |
___ |
___ |
| |
|
|
|
9 |
7 |
6 |
8 |
| |
|
|
6 |
5 |
1 |
2 |
|
+ |
1 |
3 |
0 |
2 |
4 |
| |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
| |
1 |
3 |
7 |
7 |
2 |
8 |
8 |
-
3 x 6 =
18,
Colocamos el 8 y
nos llevamos 1 , que
sumaremos al siguiente
producto.
-
3 x 5 =
15,
15 + 1 (que nos
llevábamos) = 16,
Colocamos el 6 y
nos llevamos 1 , que
sumaremos al siguiente
producto.
-
3 x 2 = 6,
6 + 1 (que nos
llevábamos) = 7,
Colocamos el 7
(Como 7 es menor que 10
ahora no nos llevamos
ninguna).
-
3 x 3 = 9,
Como no nos llevábamos
ninguna colocamos el
9.
Hemos terminado de
multiplicar 3 x 3256,
ahora seguiremos con el
2.
-
2 x 6 =
12,
Colocamos el 2 y
nos llevamos 1 , que
sumaremos al siguiente
producto.
-
2 x 5 =
10,
10 + 1 (que nos
llevábamos) = 11,
Colocamos el 1 y
nos llevamos 1 , que
sumaremos al siguiente
producto.
-
2 x 2 = 4,
4 + 1 (que nos
llevábamos) = 5,
Colocamos el 5
(Como 5 es menor que 10
ahora no nos llevamos
ninguna).
-
2 x 3 = 6,
Como no nos llevábamos
ninguna colocamos el
6.
Hemos terminado de
multiplicar 2 x 3256,
ahora seguiremos con el
4.
-
4 x 6 =
24,
Colocamos el 4 y
nos llevamos 2 , que
sumaremos al siguiente
producto.
-
4 x 5 =
20,
20 + 2 (que nos
llevábamos) = 22,
Colocamos el 2 y
nos llevamos 2 , que
sumaremos al siguiente
producto.
-
4 x 2 = 8,
8 + 2 (que nos
llevábamos) = 10,
Colocamos el 0 y
nos llevamos 1 , que
sumaremos al siguiente
producto.
-
4 x 3 =
12,
12 + 1 (que nos
llevábamos) = 13,
Como ya no tenemos más
cifras colocamos el
13.
Hemos terminado de
multiplicar 4 x 3256, y
el multiplicador (423)
no tiene más cifras.
Como el multiplicando
tiene 4 cifras (3256) y
el multiplicador 3
(423), la multiplicación
se hace en 12 pasos (4 x
3 = 12).
Ahora sólo nos queda ir
sumando cada columna.
-
la primera sólo
tiene el 8, así que
colocamos el 8 abajo.
-
la segunda columna 6
+ 2 = 8 , así que
colocamos otro 8
abajo.
-
la tercera columna 7
+ 1 + 4 = 12 , así
que colocamos el 2
abajo(y nos
llevaremos 1).
-
la cuarta columna 9
+ 5 + 2 = 16 , 16 +
1 (que nos
llevábamos) = 17,
Colocamos el 7
abajo(y nos
llevaremos 1).
-
la quinta columna 6
+ 0 = 6 , 6 + 1 (que
nos llevábamos) = 7,
Colocamos el 7
abajo(y NO nos
llevaremos nada).
-
la sexta columna
sólo tiene un 3, así
que colocamos el 3
abajo.
-
la séptima columna
sólo tiene un 1, así
que colocamos el 1
abajo.
Y ya hemos terminado.
3,256 x 423 = 1,377,288
Un millón
trescientos setenta
y siete mil
doscientos ochenta y
ocho
PARA HACER BIEN LAS
MULTIPLICACIONES ES NECESARIO
SABERSE LAS TABLAS DE MEMORIA
-
Los números que se multiplican se llaman
factores.
-
El resultado se conoce como
producto.
Distinta especie
 Los
factores siempre tienen distinta especie. Los
factores siempre tienen distinta especie.
Observa el siguiente ejemplo:
1 caja
tiene 12 lápices
de colores.
Las especies de nuestro ejemplo son caja y
lápices. Analicemos el problema:
5 cajas
tienen _______
lápices
Nos hablaban de los lápices de 1 caja y lo
desconocido es lápices de 5 cajas. Para encontrar la solución, aplicamos
multiplicación, porque 5 cajas tienen más lápices que 1 caja.
El resultado será:
12 x
5 = 60
La tabla pitagórica
La mejor forma para obtener el producto es la
multiplicación. Cuando hablamos de esta operación, existe una tabla muy
útil y fácil de construir: la Tabla Pitagórica.
En ella, hemos colocado los 13 primeros números
cardinales en forma horizontal y vertical. Llenamos cada columna con una
secuencia ascendente del número que la encabeza, empezando por el 0 y
aumentando según el número.
Por ejemplo en la columna 5, aumentamos de 5 en 5.
A continuación, observa que cada columna y fila de
un número coinciden en sus productos.
| X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
| 3 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
33 |
36 |
| 4 |
0 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
| 5 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
| 6 |
0 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
72 |
| 7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
77 |
84 |
| 8 |
0 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
88 |
96 |
| 9 |
0 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
99 |
108 |
| 10 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
| 11 |
0 |
11 |
22 |
33 |
44 |
55 |
66 |
77 |
88 |
99 |
110 |
121 |
132 |
| 12 |
0 |
12 |
24 |
36 |
48 |
60 |
72 |
84 |
96 |
108 |
120 |
132 |
144 |
¿Sabes qué hemos hecho? Las famosas tablas de
multiplicar.
Hemos anotado los 11 primeros múltiplos de cada
número.
Los múltiplos resultan de multiplicar cada número
por ¡todos los números! Son infinitos.
Con nuestra tabla podremos resolver nuestro
ejemplo.
| D.U. |
|
1 2
x 5
___ |
|
|
|
| 6 0 |
|
| Producto final |
Empezamos por las unidades:
5 veces 2 = 10
10 U. = 1 D.
Colocamos 0 en las U. y reservamos 1 D.
Multiplicamos las D: 5 x 1 = 5, y con la
reserva que teníamos: 5 + 1 = 6 D
|
Con decenas, centenas y miles
Profundizaremos el estudio de la multiplicación revisando cómo se
multiplican factores más grandes.
Revisaremos el siguiente ejemplo:
Si tenemos 1240 plantas, cada una con 25 hojas, ¿cuántas hojas tenemos
en total? |
-
Una suma abreviada: la multiplicación
-
Con decenas, centenas y miles
-
Aproximemos
-
Productos curiosos
-
Inicio
|
| U. |
M. |
C. |
D. |
U. |
|
D. |
U. |
|
Primero multiplicamos
1.240
.
5 Unidades.
El resultado son
Unidades. |
| |
1 |
2 |
4 |
0 |
x
|
2 |
5 |
|
_________________
|
|
|
|
| U. |
M. |
C. |
D. |
U. |
|
|
|
| |
6 |
2 |
0 |
0 |
|
|
|
|
U. |
M. |
C. |
D. |
U. |
|
D. |
U. |
|
Luego multiplicamos
1.240.
2 Decenas
El resultado son Decenas
El producto lo colocamos
desde la columna Decenas. |
| |
1 |
2 |
4 |
0 |
x
|
2 |
5 |
|
_________________
|
|
|
|
| U. |
M. |
C. |
D. |
U. |
|
|
|
| |
6 |
2 |
0 |
0 |
|
|
|
| 2 |
4 |
8 |
0 |
|
|
|
|
|
|
|
U. |
M. |
C. |
D. |
U. |
|
D. |
U. |
|
Para obtener el producto total,
sumamos ambos resultados. Si el factor de la derecha hubiese tenido
Centenas,
el resultado se habría puesto desde
esa columna, es decir debajo del 8 de 2.480. |
| |
|
1
|
2 |
4 |
0 |
x
|
2 |
5 |
|
_________________
|
|
|
|
|
U. |
M. |
C. |
D. |
U. |
|
|
|
| |
|
6 |
2 |
0 |
0 |
|
|
|
| + |
2
|
4 |
8 |
0 |
|
|
|
|
|
___________________
|
|
|
|
| |
3 |
1 |
0 |
0 |
0 |
|
|
|
Propiedades
La multiplicación tiene propiedades muy parecidas a las de la adición.
Veamos.
-
Tiene clausura:
todas las multiplicaciones dan un producto.
45
x
2
=
90
-
Es conmutativa:
El orden de los factores no cambia el producto.
45
x
2
=
2
x
45
90 =
90
-
Es asociativa:
Si multiplicamos 3 factores, juntamos de a 2, no importa el orden.
(3
x
4)
x
2
=
3
x
(4
x
2)
12
x
2
=
3
x
8
24 =
24
-
Tiene como elemento
neutro al 1.
Cualquier número x1
= ese número
45 x
1 = 45
-
Su elemento
absorbente, el 0: Todo número
x
0 =
0
45 x
0 = 0
-
Es distributiva con
la adición. Se junta con cada sumando. La
adición se hace con los productos.
3 x
(2+5)
= (3
x 2)+(3
x 5)
3 x
7 =
6 + 15
21 =
21
|
|
Aproximemos
En la multiplicación también se puede estimar
resultados. En este caso, conviene
aproximar por redondeo a la columna de
mayor valor.
Redondear es aproximar con una cifra seguida de ceros.
¿Qué pasa al multiplicar con una cifra seguida de ceros? Se multiplica
la cifra por el factor y se le agregan los ceros.
Un ejemplo: 5,000 x4 = 5 x4 = 20; entonces,
agregamos los 3 ceros y tenemos: 20,000
Ahora, vamos a estimar el resultado de:
349
x
6
Redondearemos la Centena: a 300 y a 400 para obtener ambos cálculos:
300
x
6
=
1,800 400
x
6
=
2,400
El resultado real estará entre
1,800 y
2,400
Así, tenemos que resultado real es:
| |
3 |
4 x |
9 6 |
|
|
| |
_________ |
|
|
| 2 |
0 |
9 |
4 |
|
|
|
-
Una suma abreviada: la multiplicación
-
Con decenas, centenas y miles
-
Aproximemos
-
Productos curiosos
-
Inicio
|
Un consejo |
Para adquirir mayor rapidez y obtener los resultados sin errores, es
importante memorizar las tablas de multiplicar. Eso se consigue
ejercitando las multiplicaciones.
Las tablas de multiplicar te servirán para toda la vida. |
|
| Pequeña prueba
1. Una caja tiene 3 lápices. ¿Cuántos
lápices habrá en 61 cajas?
A) 56
B) 66
C) 183
D) 300
|
2. En una caja hay 10 crayolas
de colores. ¿Cuántas crayolas habrá en 55 cajas?
A) 550
B) 55
C) 65
D) 450 |
|
3. Un grupo de12 compañeros compramos
15 papeletas de una rifa cada uno. ¿Cuántas papeletas tenemos ahora?
A) 21
B) 80
C) 180
D) 60
|
4. Un domingo compré 8 bolsas
de papitas a .50 centavos cada una.¿Cuánto dinero me gasté?
A) $2.95
B) $1.90
C) $4.00
D) $8.00 |
|
5. Una niña tiene 12 sacos de canicas
con 11 en cada saco, ¿cuántas tiene tiene en total?
A) 92
B) 20
C) 132
D) 88 |
|
6. Un sello de correos vale 50
centavos. ¿Cuánto valdrán 2 sellos?
A) .67 centavos
B) $1.00 dólar
C) $2.00 dólares.
D) $10.00 dólares. |
|
7. Ana Victoria tiene 6 caramelos y su
hermana Montse 18 veces más. ¿Cuántos caramelos tiene Montse?
A) 108
B) 24
C) 68
D) 118 |
|
8. Hemos comprado un carrito de $5.00
dólares, para cada uno de 2 hermanos.¿cuánto pagaremos en total?
A) $15.00 dólares
B) $10.00 dólares
C) $6.00 dólares
D) $5.50 dólares |
|
9. Una niña compró 3 libras de papas a
.50 céntavos la libra.¿Cuánto gastó en total?
A) $1.30
B) $1.20
C) $1.60
D) $1.50 |
|
10. Un grupo de 27 chicos compran
entradas para un juego de baloncesto de 8 dólares cada una. ¿Cuánto
se gastaron?
A) $35.00 dólares
B) $226.00 dólares
C) $196.00 dólares
D) $216.00 dólares |
|
Clave: Oprima su lado
izquierdo del mouse y paselo aquí debajo:
1.C 2.A 3.C 4.C 5.C 6.B 7.A 8.B 9.D 10.D |
|