Astroide
Fecha de primera versión: 24-06-2006
Fecha de última actualización:
19/04/2010
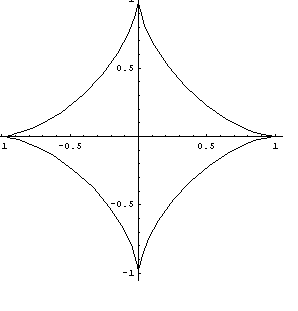La
ecuación cartesiana del Astroide es x2/3 + y2/3 = a2/3
En paramétricas: x = a cos3 t, y = a sen3 t
Supongamos una recta que corta al eje X en el punto (a,0) y al eje Y en el punto (0.b). Marquemos esos puntos sobre la recta como A y B. Ahora supongamos que la recta se desplaza manteniendo esos puntos A y B siempre sobre los ejes X e Y (podéis imaginaros una escalera apoyada en una pared y que la escalera se escurre sobre el suelo). La rama del astroide situado en el primer cuadrante de los ejes cartesianos, es la envolvente de esas rectas.
En la página http://www-groups.dcs.st-and.ac.uk/~history/Curves/Curves.html encontrarás todo sobre las curvas.