L a G r a
n E n c i c l o p e d i a I l u s t r a d a d e l P r o y
e c t o S a l ó n H o g a r

Divisores y
múltiplos
de un número
natural |
|
El origen de la palabra CÁLCULO es latino: la palabra "calculus"
significa en latín "piedra pequeña". Como era tan frecuente entre
los pueblos antiguos el sacar cuentas con la ayuda de piedritas
hechas de arcilla, el vocablo calculus pasó a convertirse en la
expresión usada para las operaciones básicas entre números
naturales. Más adelante, se usó esta palabra también para
operaciones entre otras clases de números.
Además de las piedritas y el ábaco, hubo muchos métodos para
calcular entre los antiguos que fueron realmente ingeniosos, como el
que usaban los egipcios para multiplicar.
Hay un método para multiplicar dos números mayores que 5 y menores
que 10 usando sólo los dedos de las manos. Fue utilizado en Europa
hasta hace unos 600 años y aún se usa en algunos pueblos muy
apartados de Rusia. Consiste en lo siguiente:
|
 |
Ejercicio:
Usando este método, calcula:
a)
7 x 9
b)
6 x 7
c)
9 x 6 |
Es interesante observar también
algunas curiosidades que se aprecian cuando se realizan cálculos con
piedritas, botones, o cualquier objeto pequeño y fácil de manejar.
Por ejemplo, como la multiplicación 7 x 3 consiste en sumar el 3
consigo mismo 7 veces, entonces con las piedritas se procede a
colocar 7 filas de 3 piedritas cada una se cuentan las |

|
|
piedritas y se obtiene, por
supuesto, 21. Si se ordenan de otra manera las piedritas, por
ejemplo así: |
 |
|
Es igual que antes el número de piedras, y en este caso, se han
representado 3 filas de 7 piedritas cada una, es decir: 3 x
7 = 21 se llamará a esta figura un rectángulo de piedritas,
de lados 3 y 7.
Lo que se acaba de ver claramente es que la propiedad
Conmutativa
del producto es verdadera:
|
|
|
 |
|
En el producto 3 x 7, los
números 3 y 7 se llaman los factores
de ese producto. Como 3 x 7 = 21, se dice que 3 y 7 son factores
de 21.
Para reflexionar:
¿Habrá otros
números naturales que sean factores de 21?
Para responder a esta pregunta, podríamos intentar averiguarlo de
la manera siguiente:
Tratemos de encontrar un rectángulo de 21 piedritas con lados
distintos de 3 y 7 (puedes, si lo prefieres, utilizar botones ó "taquitos"
de papel para hacer las pruebas con los rectángulos, en lugar de
usar piedritas). ¿Qué concluyes? |
| |
|
Si has acertado en tus respuestas, sabes lo que es un factor de un
número, y podrás comprender con facilidad lo que sigue. Si tus
respuestas han sido incorrectas, lee de nuevo con cuidado la
definición de factor de un número y observa el ejemplo que se da a
continuación con los factores de 21.
Los números como el 11, que tienen sólo dos factores distintos (el
mismo número y la unidad) son llamados primos.
|
Volviendo a los
rectángulos de piedritas, si se va a representar el cuadrado de un
número, por ejemplo, 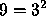 , resulta que la
figura es un cuadrado. , resulta que la
figura es un cuadrado. |
 |
|
Esta representación de los números que son el cuadrado de un número
natural, permite notar una curiosidad interesante:
|
|
|
|
Aquí se observa que cada cuadrado tiene una
cantidad de piedritas que es igual a la suma de la cantidad que
tenía el cuadrado anterior más las piedritas que hacen falta para
completar una esquina nueva.
|
Sin hacer la representación, podemos saber que 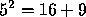 , porque hay que agregar 9 piedritas al cuadrado de la derecha.
, porque hay que agregar 9 piedritas al cuadrado de la derecha. |
 |
| para obtener
este otro: |
|
se sabe que son 9 las que agregamos, porque son 4 por cada lado y
una para la esquina.
|
|
Divisores
A los factores de un número se les llama también divisores
de ese número.
En otras palabras, si un número es divisor de otro, lo divide de
manera exacta. Por ejemplo:
7 es divisor de 14 porque 7 x 2 = 14, y por lo tanto, 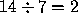 y no hay resto en esta división. Por eso se dice que es exacta.
y no hay resto en esta división. Por eso se dice que es exacta.
Si se quiere averiguar si 7 es divisor de 20, basta con dividir 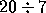 . en este caso, la división no es exacta, porque se obtiene un resto
al efectuarla. Esto quiere decir que 7 no es un divisor de 20.
. en este caso, la división no es exacta, porque se obtiene un resto
al efectuarla. Esto quiere decir que 7 no es un divisor de 20.
Para reflexionar:
1. ¿Puede ser mayor que 8 un
número que sea divisor de 8? ¿Por qué?
2. ¿Existe algún número mayor que cero que no
tenga ningún divisor?¿por qué?
3. Dado un número cualquiera, ¿cuál es el mayor
de todos sus divisores?
Responde las interrogantes en el siguiente recuadro, impríme tus
respuestas y compáralas con las du tus compañeros.
|
|
Si has respondido
correctamente estas preguntas, las nociones estudiadas hasta ahora
deben estar claras y estás preparado para comprender con facilidad
lo que sigue. Si no has respondido correctamente, hay alguna idea
relacionada con los divisores de un número que no está clara para tí,
y debes tratar de aclararla completamente antes de continuar, para
evitar futuras dificultades. |
Números Primos
Ya se ha visto que aquellos números que tienen
sólo dos divisores, el mismo número y la unidad, se llaman primos. |
|
| |
Si un número tiene más de dos divisores, se
dice que es un número compuesto.
Para reflexionar:
El número 1 no es ni primo ni compuesto |
|
Si se quisieran encontrar
todos los números primos que hay entre 1 y 100, sería bastante largo
el trabajo de detectar más de dos divisores para cada uno de los
números entre 1 y 100.
Hace más de 2.200 años, un matemático griego muy importante
llamado Eratóstenes creó un método muy sencillo y eficaz para
encontrar todos los números primos de una lista grande de números.
Su método se llamó la Criba de Eratóstenes,
y aún hoy en día, ese método es usado con computadoras para
determinar números primos.
Se describirá el método, paso a paso, para determinar todos los
números primos que hay entre 1 y 100.
|
|
Múltiplos de un número natural
|
| Si un número es
divisor de un segundo número dado, se dice que el segundo es
múltiplo
del primero. |
| Se considerarán
ahora todos los divisores y los múltiplos del número 6.
|
Divisores: 1, 2, 3, 6
Múltiplos: 6, 12, 18, 24, 30, 36, ...
|
Para determinar
los múltiplos del 6, simplemente se ha multiplicado el 6 por 1, por
2, por 3, y así sucesivamente. Podría seguirse multiplicando el 6
indefinidamente por todos los números naturales que existen, y se
seguirían obteniendo múltiplos del 6. Como no se multiplicará
indefinidamente, se indica con los puntos suspensivos que los
múltiplos de 6 no se terminan allí. En otras palabras, hay infinitos
números que son múltiplos del 6, mientras que divisores del 6 hay
solo 4, un número
finito de ellos.
Esto ocurre con cualquier número que se escoja; por muy grande que
sea un número, tendrá una cantidad finita de divisores y una
cantidad infinita de múltiplos. |