|
|
Á L G
E B R A
El Teorema de Pitágoras

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
El Teorema de Pitágoras
 Pitágoras de Samos fue un filósofo griego que vivió
alrededor del año 530 a.C., residiendo la mayor parte de su vida
en la colonia griega de Crotona, en el sur de Italia. De acuerdo con la
tradición fue el primero en probar la afirmación (teorema)
que hoy lleva su nombre: Pitágoras de Samos fue un filósofo griego que vivió
alrededor del año 530 a.C., residiendo la mayor parte de su vida
en la colonia griega de Crotona, en el sur de Italia. De acuerdo con la
tradición fue el primero en probar la afirmación (teorema)
que hoy lleva su nombre:
Si un triángulo tiene lados de longitud (a,b,c),
con los lados (a,b) formando un ángulo de 90 grados ("ángulo
recto"), tenemos que
a2 + b2
= c2
Un ángulo recto se puede definir como el ángulo formado cuando
dos líneas rectas se cruzan de tal forma que los cuatro ángulos
que forman son iguales. El teorema también se puede definir de otra
forma: si las longitudes de los tres lados (a,b,c) de un triángulo
satisfacen la relación anterior, el ángulo entre los lados
a
y b debe ser de 90 grados.
Por ejemplo, un triángulo con los lados a = 3, b
= 4, c = 5 (pulgadas, pies, metros,... lo que sea) es rectángulo
porque
a2 + b2 = 32 + 42
= 9 + 16 = 25 = c2
Los maestros de obras del antiguo Egipto pudieron conocer el triángulo
(3,4,5) y usarlo (mediante cañas o cuerdas calibradas) para construir
ángulos rectos; aún hoy en día los albañiles
usan tableros con clavos con esas longitudes que les ayudan a alinear una
esquina.
Existen muchas pruebas, y las más fáciles son probablemente
las que están basadas en el álgebra, usando las igualdades
elementales presentadas en la sección precedente, a saber
(a + b)2 = a2 + 2ab + b2
(recuerde que 2ab significa 2 veces a
veces b). Por ejemplo
152 = (10 + 5)2
= 102 + (2)(10)(5) + 52
= 100 + 100 + 25 = 225
y
(a - b) 2 = a2 - 2ab + b2
Por ejemplo:
52 = (10 - 5)2
= 102 - (2)(10)(5) + 52
= 100 - 100 + 25 = 25
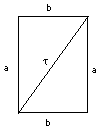
También es necesario conocer algunas áreas simples: el área
de un rectángulo es (longitud) por (altura), de tal forma que el
área del presentado arriba es ab. Una diagonal lo divide
en dos triángulos rectángulos siendo los lados cortos a
y b, y el área de ese triángulo es, por consiguiente,
(1/2) ab.
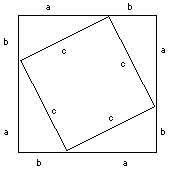
Vea el cuadrado de la izquierda construido por cuatro triángulos
(a,b,c). la longitud de cada lado es (a+b) y, por lo tanto,
el cuadrado tiene un área de (a+b)2.
No obstante, el cuadrado se puede a su vez dividir en cuatro triángulos
(a,b,c) más un cuadrado de lado c en el centro (en
rigor, también debemos de probar que es un cuadrado, pero
nos saltaremos esto). El área de cada triángulo, como se
mostró anteriormente, es (1/2)ab, y el área del cuadrado
es c2. Como el cuadrado grande es igual a la suma de
todas sus partes
(a + b) 2 = (4)(1/2)(a)(b) + c2
Usando la igualdad para (a + b)2 y multiplicando (4)(1/2)
= 2
a2 + 2ab + b2 = 2ab + c2
Reste 2ab de ambos lados y obtendrá
a2 + b2 = c2
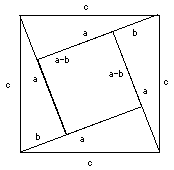
Se puede mostrar el mismo resultado usando un cuadrado diferente, de
área
c2. Como muestra el dibujo de la derecha,
esa área puede dividirse en cuatro triángulos como los anteriores,
más un pequeño cuadrado de lado (a-b). Obtenemos
c2 = (4)(1/2)(a)(b) + (a-b) 2
= 2ab + (a2 - 2ab + b2)
= a2 + b2 Q.E.D.
Q.E.D. simboliza "quod erat demonstrandum," en latín "lo que
queda demostrado," que en los libros de geometría, tradicionalmente,
marcaban el final de una demostración. La importancia del trabajo
de Pitágoras y de los siguientes maestros de geometría griegos,
especialmente Euclides, no fue solo lo que probaron, sino el método
que desarrollaron: comenzar desde algunas afirmaciones básicas ("axiomas")
y deducir mediante la lógica sus consecuencias más complicadas
("teoremas"). Los matemáticos aún siguen ese modelo.
|
|