T e m a
d e l d í a
con
Proyecto Salón Hogar


Geometría
Indice
1. Poliedro
2. Prisma
3. Poliedros Regulares
4. Buckminsterfullereno o Fullereno C60
5. Pirámide
6. Triángulo
7. Teorema De Euler
8. Teorema de Pitágoras
9. Formula De Herón
1. Poliedro
Porción de espacio limitada por polígonos planos. Sus elementos característicos son las caras, las aristas y los vértices:
Las caras son los polígonos que la limitan.
Las aristas son los lados de las caras, y limitan dos caras contiguas.
Los vértices son los de las caras. En cada vértice de un poliedro concurren tres o más caras.
Un poliedro se llama convexo si todo él está en el mismo semiespacio respecto al plano de cada una de sus caras.
Poliedro cóncavo es el que tiene alguna cara cuyo plano atraviesa a la figura.
Poliedro simple es el que no tiene orificios que lo atraviesen. En todo poliedro simple se cumple el teorema de Euler
2. Prisma
Poliedro limitado por dos polígonos iguales, llamados bases, situados en planos paralelos, y por varios paralelogramos, llamados caras laterales.
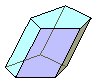
Se llama altura del prisma a la distancia entre los planos en que se sitúan sus bases.
Un prisma se llama triangular, cuadrangular, pentagonal… según que sus bases sean triángulos, cuadriláteros, pentágonos…
Un prisma recto es el que tiene sus caras laterales perpendiculares a las bases:
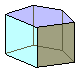
En el prisma recto, las caras laterales son todas ellas rectángulos. Si sus bases son polígonos regulares, el prisma se llama regular.
Un prisma oblicuo es el que tiene sus aristas laterales oblicuas a los planos de las bases.
Los prismas cuyas bases son paralelogramos se llaman paralelepípedos. En un paralelepípedo, sus seis caras son paralelogramos.
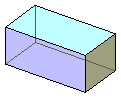
Se llama área lateral de un prisma al área de todas sus caras
laterales. El área lateral de un prisma recto es:
Alat = perímetro de la base · altura
El área total es la suma del área lateral con las áreas de las
bases:
Atot = área lateral + 2 · área de la base
El
volumen de un prisma cualquiera es igual al área de la base por
la altura:
V = área de la base · altura
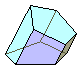
Cada uno de los dos cuerpos geométricos que se obtienen al partir un
prisma por un plano que corta a todas sus aristas laterales se llama
tronco de prisma.
3. Poliedros Regulares
Un poliedro regular es aquel cuyas caras son polígonos
regulares iguales y en cada uno de sus vértices concurren el mismo
número de caras. Sólo existen cinco tipos de poliedros regulares:
Tetraedro regular: 4 caras triangulares, que concurren tres en cada
vértice. Tiene 4 vértices y 6 aristas.
Cubo: 6 caras cuadradas, que concurren tres en cada vértice. Tiene 8
vértices y 12 aristas.
Octaedro: 8 caras triangulares, que concurren cuatro en cada
vértice. Tiene 6 vértices y 12 aristas.
Dodecaedro: 12 caras pentagonales regulares, que concurren tres en
cada vértice. Tiene 20 vértices y 30 aristas.
Icosaedro: 20 caras triangulares, que concurren cinco en cada
vértice. Tiene 12 vértices y 30 aristas
Dos poliedros regulares se llaman conjugados si cada uno de ellos se
obtiene del otro uniendo mediante segmentos los puntos
medios de cada dos caras contiguas. Así, el tetraedro es
conjugado de sí mismo, el dodecaedro es conjugado del icosaedro y el
cubo lo es del octaedro:
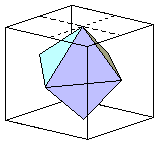
Tetraedro
Poliedro con cuatro caras que, necesariamente, han de ser
triángulos. Es, por tanto, una pirámide triangular:
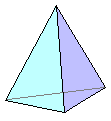
Si las cuatro caras de un tetraedro son triángulos equiláteros,
entonces se llama tetraedro regular y es uno de los cinco poliedros regulares.
Habitualmente, al hablar del tetraedro se hace referencia al tetraedro regular.
El área de un tetraedro regular en
función de su arista es:
A= a2 Ö 3
Su volumen es:
V = a3 /12
Cubo
Poliedro regular formado por seis caras cuadradas.

El cubo es un ortoedro (sus caras son perpendiculares) con todas las
aristas iguales.
El área total de un cubo de arista a es
A = 6a2
Su volumen es
V = a3
La longitud de su diagonal es: D= a Ö
3
El cubo se llama también hexaedro regular o, simplemente, hexaedro.
Octaedro
Poliedro de ocho caras. Se suele designar genéricamente así al octaedro regular,
poliedro formado por ocho triángulos equiláteros idénticos:
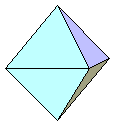
El área de las caras de un octaedro en función de su arista, a, es:
A= 2a2 Ö 3
Su volumen es:
V = a3/3
Dodecaedro
Poliedro regular formado por doce caras pentagonales:
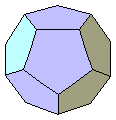
El área de un dodecaedro de arista a es:
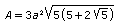
Su volumen es:
V = a3(15 + 7)/4
Icosaedro
Poliedro regular formado por veinte caras triangulares:
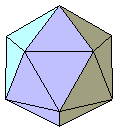
El área de un icosaedro es:
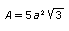
Su volumen es:
V = 5a3(3 + )/12
4. Buckminsterfullereno o Fullereno C60
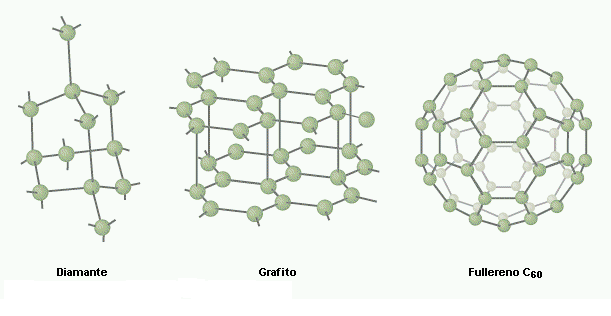
Una forma natural o alotrópica del
carbono. Durante muchos años se pensó que el elemento carbono
existía en dos formas alotrópicas (o distribuciones distintas de los
átomos), el diamante y el grafito. El diamante es un sólido en el
que cada
átomo de carbono se une a otros cuatro, y esta
distribución se extiende por todo el cristal dando lugar a un
sólido rígido y duro. En el grafito, los átomos de carbono se unen
formando anillos hexagonales en láminas planas superpuestas, y el
resultado es un sólido escurridizo. El carbono es uno de los
elementos más investigados, por lo que fue una gran sorpresa el
descubrimiento en 1985 de una
familia entera de formas alotrópicas distintas, los fullereros.
Este descubrimiento fue el resultado de las
investigaciones sobre la formación de compuestos de carbono en
el interior de las estrellas realizadas por el británico Harold W.
Kroto, en colaboración con los estadounidenses Robert F. Curl y
Richard E. Smalley; por ello, los tres científicos recibieron el
Premio Nobel de
Química en 1996.
El buckminsterfullereno, la forma alotrópica más conocida del
grupo de los fullerenos, consiste en 60 átomos de carbono unidos
para formar una molécula C60 de hexágonos y pentágonos dispuestos en
forma casi esférica, como la envoltura de una pelota de fútbol. La
molécula recibe ese nombre porque su
estructura se parece a las elaboradas
estructuras geométricas inventadas por el arquitecto
estadounidense Richard Buckminster Fuller. Existen otros fullerenos
que poseen más átomos de carbono y sus formas son versiones
alargadas del buckminsterfullereno inicial (en forma de pelota). Con
el aumento en la
producción de buckminsterfullereno, se llegó a obtener una forma
sólida, la fullerita. En este sólido amarillo transparente, las
moléculas forman una especie de conjunto de balas de cañón en una
distribución compacta. Ahora existen también versiones tubulares de
fullerenos en forma sólida.
Originalmente se preparaba el buckminsterfullereno en un haz
molecular y sólo podían conseguirse pequeñas cantidades. Sin
embargo, pronto se vio que podían obtenerse grandes cantidades de
moléculas en un arco eléctrico entre dos electrodos de carbono en
atmósfera de helio. Actualmente se sabe que es probable que el
buckminsterfullereno se forme en llamas tiznadas, y existe incluso
la posibilidad de que abunde en
el Universo, particularmente cerca de las estrellas rojas
gigantes.
Cuando los fullerenos empezaron a ser abundantes, los químicos
comenzaron a investigar sus propiedades. Se piensa que los
fullerenos podrían dar origen a un nuevo campo de la química, del
mismo modo que la química orgánica aromática surgió a raíz del
descubrimiento del benceno 150 años atrás. Una de las propiedades
más sorprendentes de los fullerenos es que se pueden introducir
átomos de elementos en el hueco existente en la 'jaula' de átomos de
carbono; así se puede obtener una versión de 'envoltura contraída'
de cada elemento del
sistema
periódico. Cuando se introducen átomos de metal en los tubos
tipo fullereno mencionados anteriormente, el material resultante es
como un alambre aislado unidimensional. Otra
propiedad importante es que ciertos compuestos de
buckminsterfullereno (en especial el K3C60) son superconductores a
bajas temperaturas. Se ha averiguado que los derivados del
buckminsterfullereno son biológicamente
activos y se están utilizando para atacar
el cáncer: se cree que las moléculas en forma de pelota de
fútbol pueden introducirse en los emplazamientos activos de las
enzimas y bloquear su acción.
5. Pirámide
Poliedro limitado por una base, que es un polígono cualquiera, y varias
caras laterales, que son triángulos con un vértice común llamado
vértice de la pirámide.
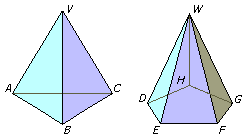
La altura de la pirámide es la distancia del vértice a la base. Una
pirámide se llama triangular, cuadrangular, pentagonal… según que su
base sea un triángulo, un cuadrilátero, un pentágono…
Una pirámide es regular si su base es un polígono regular y el
vértice se proyecta (cae perpendicularmente) sobre el centro de la
base. En una pirámide regular las caras laterales son triángulos
isósceles cuyas alturas se llaman apotemas de la pirámide.
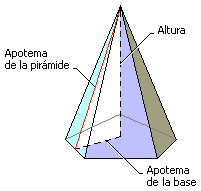
El área lateral de una pirámide regular (suma de las áreas de las caras
laterales) es:

y el área total:
Atot = Alat + Abase
El volumen de una pirámide es la tercera parte del
producto del área de la base por la altura:
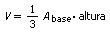
Tronco De Pirámide
Un tronco de pirámide es el poliedro comprendido entre la base de la
pirámide y un plano que corta a todas las aristas laterales.
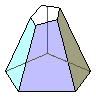
Si el plano es paralelo al plano de la base se dice que el tronco es de
bases paralelas. La distancia entre las bases es la altura del
tronco. Un tronco de bases paralelas de una pirámide regular está
formado por dos bases, polígonos regulares semejantes, y varias
caras laterales que son trapecios isósceles. Las alturas de estos
trapecios se llaman apotemas de estos troncos.
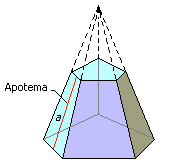
El área lateral de un tronco de pirámide de bases paralelas es:
Alat = semisuma de los perímetros de las bases · apotema
El volumen de un tronco de pirámide, cuyas bases son paralelas y
tienen superficies B y B’, y cuya altura es h, se obtiene mediante
la fórmula siguiente:
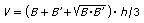
6. Triángulo
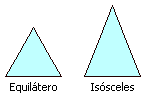
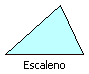
Polígono de tres lados. Según la longitud de sus lados, los
triángulos se clasifican en equiláteros, si sus tres lados
son iguales, isósceles, si tienen dos lados iguales, y escálenos, si
los tres lados son distintos.
La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos
son, necesariamente, agudos. El tercero puede ser también agudo, o
bien recto u obtuso. Si los tres ángulos son agudos el triángulo se
llama acutángulo, si tiene una ángulo recto, rectángulo y
obtusángulo si el mayor de sus ángulos es obtuso.

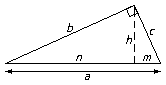
Triángulos Rectángulos
Los triángulos rectángulos cumplen una serie de relaciones métricas
importantes entre sus lados.
Los lados de un triángulo rectángulo que forman el ángulo recto, b y
c, se llaman catetos y el tercer lado, a, (opuesto al ángulo recto)
es la hipotenusa. El teorema de Pitágoras relaciona los dos catetos
y la hipotenusa: en un triángulo rectángulo, el cuadrado de la
hipotenusa es igual a la suma de los cuadrados de los catetos:
a2 = b2 + c2
Otra relación importante que se cumple en un triángulo rectángulo es
el teorema del cateto: el cuadrado de cada cateto es igual al
producto de la hipotenusa por su proyección sobre ella, es decir,
c2 = a · m, b2 = a · n
Alturas De Un Triángulo
Se llama base de un triángulo a cualquiera de sus lados. El segmento
perpendicular desde un vértice a la base opuesta o a su prolongación
se llama altura. Un triángulo tiene, pues, tres bases a, b, c, y las
tres alturas correspondientes, ha, hb y hc.
En un triángulo rectángulo el cuadrado de la altura sobre la
hipotenusa es igual al producto de los dos segmentos en que la
divide:
h2 = m · n
Esta relación se conoce como teorema de la altura.
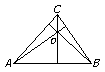
Las tres alturas de un triángulo (o sus prolongaciones) se cortan en
un punto llamado ortocentro. Si el triángulo es acutángulo, el
ortocentro es interior al triángulo.
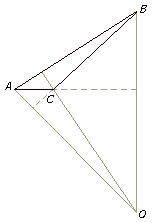
En un triángulo rectángulo, cada cateto puede ser considerado como base
y como altura. El ortocentro es, por tanto, el vértice del ángulo
recto. Si el triángulo es obtusángulo el ortocentro se obtiene,
prolongando las alturas, fuera del triángulo.
Medianas De Un Triángulo
Se llama mediana de un triángulo a cada uno de los tres segmentos que unen
un vértice con el punto medio del lado opuesto. Las tres medianas de
un triángulo se cortan en un punto que se llama baricentro.
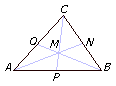
El baricentro corta a cada mediana en dos segmentos, uno de ellos la
mitad del otro:
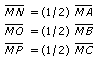
Circunferencia Inscrita
Las bisectrices de los tres ángulos de un triángulo se cortan en un punto
que se llama incentro porque es el centro de la circunferencia
inscrita que es tangente a los tres lados del triángulo. Ésta es la
mayor circunferencia contenida en el triángulo.
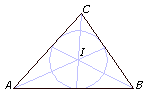
Circunferencias Exinscritas
La bisectriz interior de un ángulo se corta con las dos bisectrices
exteriores de los otros dos ángulos en un punto llamado exincentro,
y que es centro de una circunferencia (exinscrita) tangente a un
lado y a la prolongación de los otros dos.
Un triángulo tiene, pues, tres circunferencias exinscritas.
Circunferencia Circunscrita
Las mediatrices de los lados de un triángulo se cortan en un punto
llamado circuncentro porque es centro de la circunferencia
circunscrita que pasa por los tres vértices del triángulo. Esta es
la menor circunferencia que contiene al triángulo.
Área De Un Triángulo
El área de un triángulo de lados a, b, c, y alturas correspondientes ha, hb y hc
es:
A = (1/2)a · ha = (1/2)b · hb = (1/2)c · hc
Si se conocen las longitudes de los tres lados, a, b, c, el área se puede
calcular mediante la siguiente fórmula, llamada fórmula de Herón:
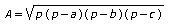
en donde p = (a + b + c)/2 es el semiperímetro del triángulo.
7. Teorema De Euler
Teorema que relaciona el número de caras, vértices y aristas de un
poliedro simple (sin orificios) cualquiera.
Establece lo siguiente: en un poliedro simple, el número de caras,
C, más el número de vértices, V, es igual al número de aristas, A,
más dos. Es decir:
C + V = A + 2
8. Teorema de Pitágoras
Teorema que relaciona los tres lados de un triángulo rectángulo, y que
establece que el cuadrado del lado mayor (hipotenusa) es igual a la
suma de los cuadrados de los otros dos lados (catetos).
El teorema de Pitágoras permite calcular uno de los lados de un
triángulo rectángulo si se conocen los otros dos. Así, permite
calcular la hipotenusa a partir de los dos catetos:
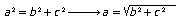
o bien, calcular un cateto conocidos la hipotenusa y el otro cateto:
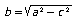
9. Formula De Herón
Fórmula que sirve para calcular el área, A, de un
triángulo en función de sus lados, a, b, c:
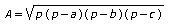
siendo p el semiperímetro: p = (a + b + c)/2.
Por ejemplo, si los lados de un triángulo miden a = 7 cm, b = 11 cm,
c = 8 cm, entonces el semiperímetro es p = (7 + 11 + 8)/2 = 13 cm y
su área es:
Trabajo enviado por:
Frank Alejandro Zapata Mesa
www.proyectosalonhogar.com