Circunferencia
Fecha de primera versión: 02-04-98
Fecha de última actualización:
19/04/2010
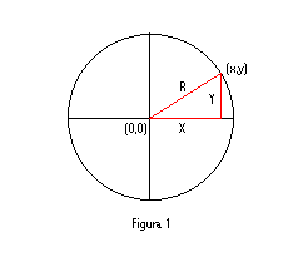
La demostración de la ecuación de una circunferencia de centro el origen y radio R es muy sencilla.
Sea (x, y) un punto cualquiera de la circunferencia. Como veis en la figura se forma un triangulo rectángulo y entonces x2 + y2 = R2. Esa es la ecuación de la circunferencia.
Si dividimos esta ecuación por R2, queda x2/R2 + y2/R2 = 1.
Si el centro de la circunferencia está en el punto de coordenadas (a,b)
la ecuación de la circunferencia es:
(x -a)2 + (y-b)2 = R2
Para comprender la ecuación de la circunferencia en paramétricas, supongamos que un punto recorre la circunferencia con velocidad angular constante, partiendo del punto (R,0) en sentido contrario a las agujas del reloj y supongamos, por simplicidad, que en cada unidad de tiempo t, el ángulo recorrido es 1º. Es fácil deducir que las coordenadas del punto (x,y) son: x = R.cos t, y = R.sen t. Estas son las ecuaciones parámetricas (en este caso el parámetro es el tiempo, t) de la circunferencia.
La longitud de la circunferencia es L = 2pR.
El área de la superficie que está dentro de la circunferencia (círculo) es A = p R2.
La circunferencia es una de las secciones del cono, cuando el plano que corta el cono, lo hace perpendicular al eje del cono.
Potencia de un punto respecto a una circunferencia
Desde un punto P, exterior a una circunferencia, trazamos dos segmentos
que cortan a la circunferencia en los puntos A, B, C y D.
Se cumple que PA.PB = PC.PD
La potencia de un punto P de coordenadas x, y respecto a una circunferencia de centro (a,b) y radio R es (x0 - a)2 + (y0 - b)2 - R2
Eje radical de dos circunferencias
Dadas dos circunferencias, el lugar geométrico de los puntos del plano que tienen la misma potencia respecto a ambas circunferencias, es una recta y se llama eje radical.
Siendo las ecuaciones de las circunferencias:
x2 + y2 + Ax + By + C = 0
x2 + y2 + A'x + B'y + C' = 0
la ecuación del eje radical es: (A - A')x + (B - B')y + (D - D') = 0
En esta dirección encontrarás todo sobre las curvas.