| |
PROPORCIONALIDAD

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
Registrate
aquí
Entrar a exámenes
de:
Contenido Revisado 
|
|
|
|
|
Los arquitectos en
la Grecia antigua tenían muy en cuenta las
proporciones a la hora de diseñar los edificios
importantes de la ciudad. Había una proporción
en particular que era muy especial para quienes
diseñaban las edificaciones. Se puede decir que
era la preferida. Fue incluso llamada la
proporción divina, o proporción áurea, y el
número que la representaba era llamado el número
de oro. En el diseño de una fachada rectangular
como la siguiente, si la medida de la altura es
a y la medida del ancho es b,
entonces la proporción entre a y b
( para que sea la proporción áurea) debe cumplir
lo siguiente: |
|
|
|
|
Esa misma
proporción se encuentra en algunos triángulos
contenidos en el pentágono regular, considerado
por los pitagóricos un símbolo universal de
salud. belleza y amor. |
|
|
|
Por ejemplo, los segmentos EG y FG
guardan entre ellos la proporción áurea, porque
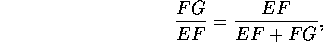
Es decir:
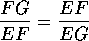
|
|
Como esta
proporción, existen en total 20 dentro del
pentágono regular.
Además, el
pentágono FGIHJ que se construye al
trazar las diagonales del pentágono ABCDE
es también regular, y si se trazan las
diagonales de FGIHJ obtenemos otra
estrella de cinco puntas como la primera. Este
proceso se lleva a cabo sucesivamente tantas
veces como se desee y siempre se obtendrán
pentágonos regulares dentro de estrellas de
cinco puntas, con infinidad de proporciones
áureas por dentro. |
| |
|
|
|
En
el lenguaje común se expresa la idea de
proporción con cierta frecuencia. Por
ejemplo:
1) "La proporción de agua
requerida para la preparación de un jugo a
partir de un concentrado está especificada en
las instrucciones de preparación del producto''.
2) "La reacción de Carlitos
ante mi crítica fue desproporcionada''.
3) "El diseño de este edificio
guarda proporciones armoniosas''.
4) "El sueldo mensual de cada
trabajador es proporcional al número de horas
semanales que trabaja''.
En
el ejemplo 1), se usa la
palabra "proporción'' para señalar la cantidad
de agua que debe usarse para diluir cada
lata o cartón de jugo concentrado en la
preparación de jugo para el consumo. Por
ejemplo, en las instrucciones podría leerse:
"Mezcle 4 vasos de agua por cada lata de jugo
concentrado".
La
idea de proporción, en este caso, se refiere a
la relación que debe mantenerse entre la
cantidad de jugo concentrado y la cantidad de
agua que se usará para diluirlo. Se están
comparando dos cantidades: la de jugo
concentrado con la de agua necesaria para su
preparación.
Si
se desea preparar jugo con 2 latas de
concentrado, ¿cuántos vasos de agua se usarían?
En
el ejemplo 2), se está
comparando una crítica a Carlitos con su
reacción. Al decir que ésta fue
"desproporcionada'', generalmente se quiere
expresar que la reacción fue mucho más violenta
que la crítica que la generó. De nuevo, se están
comparando dos magnitudes o cantidades: la
"cantidad'' de ira, violencia o severidad que
hubo en la crítica, con la que hubo en la
reacción.
En
el ejemplo 3), se habla de
"proporciones armoniosas'' en una edificación.
Una vez más, la palabra "proporción'' se refiere
aquí a una relación o comparación entre las
medidas del edificio. Podría ser la relación
entre la altura y el ancho de la fachada
principal, entre la altura y el ancho de las
ventanas, etc.
Es
muy importante notar que una misma proporción
puede darse entre las medidas de un rectángulo
pequeño así como entre las medidas de otro mucho
más grande. Así, por ejemplo, la proporción
entre el lado menor y el lado mayor en los
siguientes rectángulos es
 .
. |
| |
|
|
en ambos rectángulos, el lado mayor mide el
doble de lo que mide el lado menor.
|
|
En el ejemplo
4), se dice que el sueldo de
cada trabajador es proporcional al número de
horas semanales que trabaja. Supongamos que un
trabajador labora 20 horas semanales. ¿Qué dato
sería necesario conocer para determinar el
sueldo mensual del trabajador?
Se observa en
los cuatro ejemplos anteriores que el
significado de la palabra PROPORCIÓN tiene que
ver con la comparación de dos cantidades.
Cuando se
comparan dos cantidades, puede intentarse
precisar qué tanto mayor es una que la otra
diciendo, por ejemplo, que una de ellas es es el
doble de la otra. En este caso, se está
estableciendo una proporción entre las
dos cantidades.
Por ejemplo, si
se dice que un grupo de jóvenes hay tres veces
más muchachas que muchachos, se está expresando
la proporción entre muchachas y muchachos que
hay.
Si en ese grupo
hay 14 varones, entonces habrá el triple de
chicas, es decir, el número de chicas es:
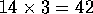
Si en otro
grupo de jóvenes hay 5 varones y la proporción
es la misma que antes, se concluye que hay
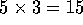 muchachas.
muchachas.
Se tienen
entonces, dos grupos distintos de jóvenes, con
distinto número de personas, pero ambos con la
misma proporción entre chicos y
chicas. Esa proporción se expresa mediante la
fracción
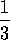
como se ha
dicho que por cada chico habrá 3 chicas, con el
número 1 del numerador se está expresando la
cantidad de muchachos, y con el 3 del
denominador, la cantidad de muchachas que habrá
por la cantidad de chicos en el numerador. Esto
se escribe así porque se habló de proporción
entre chicos y chicas (al nombrar primero a los
varones, el número que corresponde a estos va en
el numerador).
Para cada uno
de los grupos mencionados arriba, se escribirá
en una fracción las cantidades de chicos y
chicas en el numerador y el denominador
respectivamente:
Primer grupo:
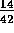
Segundo grupo:
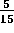
Obsérvese ahora
que
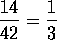
y
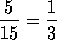
es decir,
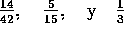 son fracciones equivalentes.
son fracciones equivalentes. |
Ejercicio:
si quisiéramos ahora saber qué cantidad
de muchachos habría en un grupo que tenga la
proporción
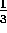 entre chicos y chicas, y que tiene 90
muchachas, ¿qué operación necesitaríamos
hacer?
entre chicos y chicas, y que tiene 90
muchachas, ¿qué operación necesitaríamos
hacer?
Considerando
de nuevo el ejemplo 1), si una lata de jugo
contiene la misma cantidad de líquido que un
vaso, entonces la proporción entre jugo y
agua es
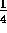 ,
según lo que indican las instrucciones de
preparación. ¿Cuántos vasos de agua habrá
que añadir a 5 vasos de jugo concentrado
para preparar jugo diluido en esa misma
proporción? ,
según lo que indican las instrucciones de
preparación. ¿Cuántos vasos de agua habrá
que añadir a 5 vasos de jugo concentrado
para preparar jugo diluido en esa misma
proporción?
Observando el
ejemplo anterior, se concluye lo siguiente:
lo único que hay que hacer es encontrar el
denominador de una fracción EQUIVALENTE a
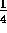 con numerador 5. En este caso, como
con numerador 5. En este caso, como
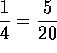 , el número buscado es 20. Habrá que añadir
20 vasos de agua a los 5 vasos de jugo
concentrado.
, el número buscado es 20. Habrá que añadir
20 vasos de agua a los 5 vasos de jugo
concentrado.
Una manera de
encontrar la respuesta a la pregunta
anterior es la siguiente: se plantea la
ecuación

para evitar
que la x esté en el denominador de
una fracción, se multiplican ambos miembros
de la igualdad por x y se obtiene:

Multiplicando
ambos miembros por 4:


para el que
recuerde la "Regla de Tres'', será útil
observar que puede usarse también en este
caso y obtenerse el mismo resultado:


La solución se
obtiene así:

|
|
Otro ejemplo:
para preparar una cierta masa, se sabe que la
proporción entre agua y harina (atención al
orden en que se nombran) es de
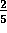 .
Eso significa que para cada 5 tazas de harina
deben agregarse 2 tazas de agua. Si se quiere
preparar masa con otra medida, por ejemplo, con
cucharadas, también debe mantenerse la
proporción de 2 cucharadas de agua por cada 5
cucharadas de harina. .
Eso significa que para cada 5 tazas de harina
deben agregarse 2 tazas de agua. Si se quiere
preparar masa con otra medida, por ejemplo, con
cucharadas, también debe mantenerse la
proporción de 2 cucharadas de agua por cada 5
cucharadas de harina.
Si
se quiere preparar masa con 15 tazas de harina,
¿cuántas tazas de agua habrá que agregar?
Usando el método del planteamiento de la
ecuación, se obtiene:

como en la fracción
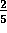 el numerador representa la cantidad de agua y el
denominador, la cantidad de harina, de la misma
manera debe ubicarse en
el numerador representa la cantidad de agua y el
denominador, la cantidad de harina, de la misma
manera debe ubicarse en
 , el denominador 15, que es la cantidad de
harina, y el numerador x, que es la cantidad de
agua que se quiere determinar.
, el denominador 15, que es la cantidad de
harina, y el numerador x, que es la cantidad de
agua que se quiere determinar.
Resolviendo,



se
necesitan 6 tazas de agua para amasar 15 tazas
de harina, manteniendo la proporción dada.
Usando la Regla de Tres:


Ahora, se resuelve:


Puede verse ahora que la "Regla de Tres" no es
más que una manera de resolver ecuaciones
surgidas de problemas relativos a PROPORCIONES.
|
|
|
|
Si
has acertado en tus respuestas, continúa tu
lectura. Si no, revisa de nuevo los
razonamientos empleados por ti para que detectes
el error cometido. Puede ser necesario que leas
de nuevo las ideas básicas en torno a
proporciones, que han sido expuestas hasta aquí.
En
algunos casos se da la proporción de una PARTE
en relación a la TOTALIDAD. Por ejemplo, en el
ejercicio anterior, la proporción entre vinagre
y agua es de
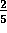 ,
se tiene que: ,
se tiene que: |
|
|
2 litros de vinagre + 5
litros de agua = 7 litros de agua
con vinagre
|
|
Entonces, la proporción de agua con la
totalidad es de 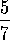 La proporción de vinagre con la totalidad es
de
La proporción de vinagre con la totalidad es
de 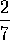
Cuando se compara una parte con la totalidad
sólo se nombra a la parte, por ejemplo, se
diría: La proporción de vinagre en la mezcla
es de
 , y la proporción de agua es de
, y la proporción de agua es de
 .
.
En el ejemplo del grupo de jóvenes, por cada
varón hay 3 chicas, es decir, que en un
grupo de

jóvenes, 1 es varón y 3 son muchachas.
Luego, la proporción de muchachas es
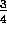 , y la proporción de varones es
, y la proporción de varones es
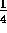 .
.
cuando se habla de proporción y sólo se
nombra a una parte, se está refiriendo a la
proporción entre esa parte y el todo.
A continuación, otro ejemplo. Supongamos que
se dice que en una población, la proporción
de analfabetas es de
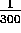 .
Esto quiere decir que de cada 300
individuos, 1 es analfabeta, es decir, no
sabe leer ni escribir. Si esa población
tiene 6.000.000 de habitantes, y se quiere
saber cuántos saben leer y escribir, se
plantea una ecuación que permita encontrar
el número de analfabetas que hay, usando la
información que ya se tiene: por cada 300
habitantes, 1 es analfabeta. .
Esto quiere decir que de cada 300
individuos, 1 es analfabeta, es decir, no
sabe leer ni escribir. Si esa población
tiene 6.000.000 de habitantes, y se quiere
saber cuántos saben leer y escribir, se
plantea una ecuación que permita encontrar
el número de analfabetas que hay, usando la
información que ya se tiene: por cada 300
habitantes, 1 es analfabeta.

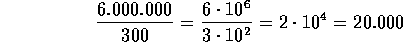
Entonces hay 20.000 analfabetas, por lo
tanto, hay
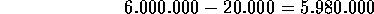
personas que saben leer y escribir en esa
población.
|
|
|
Es importante que lo expuesto hasta aquí sea
muy claro para ti, para que lo que se expone
a continuación sea también asimilado con
facilidad.
Porcentajes
Cuando se habla de porcentajes, en realidad
se está hablando de proporciones entre una
parte y la totalidad. Por ejemplo:
si se dice que el 12% de los estudiantes del
liceo son nuevos este año, lo que se está
diciendo es que por cada 100 estudiantes, 12
son nuevos, es decir, la PROPORCIÓN de
alumnos nuevos es de
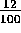 . Si en el liceo hay 600 estudiantes, para
determinar el número exacto de alumnos
nuevos, puede usarse la Regla de Tres:
. Si en el liceo hay 600 estudiantes, para
determinar el número exacto de alumnos
nuevos, puede usarse la Regla de Tres:


por lo tanto,
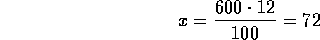
Pero también puede plantearse directamente
la ecuación siguiente:

Resolvemos:


|
|
Esta es, entonces, otra manera de resolver la
ecuación original, que también es correcta.
Se
resolverán a continuación otras ecuaciones que
exigen un conocimiento adecuado acerca de las
operaciones en Q, para su apropiada resolución.
Como se ha visto antes, no hay una única vía
correcta para resolver estas ecuaciones, pero sí
una única solución correcta.
|
|
|
|
|