| |
RADICACIÓN
|
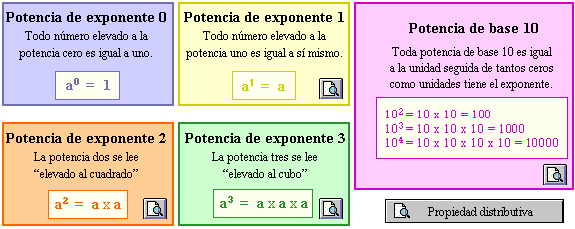
La potenciación
es el producto de varios factores iguales. Para abreviar la
escritura, se escribe el factor que se repite y en la parte
superior derecha del mismo se coloca el número de veces que
se multiplica. La operación inversa de la potenciación se denomina
radicación. |
 |
|
 |
|
|
|
|
|
|
La visión del Universo que tenían el gran sabio
griego Pitágoras de Samos y sus discípulos, los
llamados pitagóricos, estaba dominada por sus
ideas filosóficas acerca del número. Decían que
el número natural y las proporciones entre
números naturales gobernaban todo cuanto
existía.
Un
descubrimiento hecho por los mismos pitagóricos
demostró que esta afirmación era falsa.
Descubrieron la existencia de un número que no
era natural y tampoco se podía expresar como
fracción alguna.
Todo comenzó
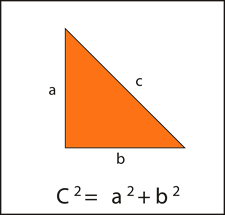
con el llamado Teorema de Pitágoras. Se llama
Teorema a toda afirmación matemática importante
que es demostrada de manera rigurosa,
irrefutable. El Teorema de Pitágoras afirma que,
en todo triángulo rectángulo, el lado mayor,
llamado hipotenusa, elevado al cuadrado, es
igual a la suma de los cuadrados de los otros
dos lados, llamados catetos.
|
 |
|
|
Se sabe que
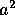es igual al área del cuadrado cuyo cuyo lado
es a (potenciación en N
). Así, lo que el Teorema de Pitágoras
afirma es lo siguiente: las áreas de los
cuadrados cuyos lados son a y b,
al sumarse, dan el área del cuadrado cuyo
lado es c.
|
|
En
todos los triángulos rectángulos quizás el de
apariencia más sencilla fue el que produjo entre
los pitagóricos la gran conmoción de presentar
la existencia de una medida que no era
expresable como un número natural ni como una
fracción.
El
triángulo cuyos catetos son ambos de medida 1
fue el que originó el derrumbe de toda una
teoría filosófica.
El
triángulo en cuestión es el de la derecha.
|
|
|
|
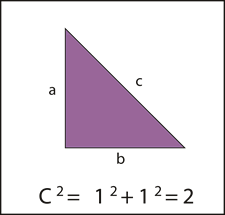
El
Teorema de Pitágoras asegura que
.
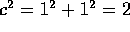Usando un método muy sencillo, los pitagóricos
intentaron encontrar números naturales m,n tales
que
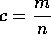, sin lograrlo nunca. La idea era la siguiente:
se
divide un cateto en segmentos de igual longitud
(longitud u) |
|
|
Se
intentaba dividir la hipotenusa también en segmentos de
longitud u, pero siempre sobraba un segmento de longitud
menor que u:
|
|
|
|
En vista de que había un segmento sobrante, se escogía
una medida para el segmento que fuera la mitad de la
medida anterior, con la esperanza de que no hubiera
ningún segmento sobrante en la hipotenusa. Pero no
funcionaba (ver imagen de la izquierda) |
Si hubieran encontrado un segmento que cupiera una
cantidad exacta de veces tanto en la hipotenusa como en
los catetos, digamos, 13 veces en la hipotenusa y 8
veces en los catetos, se tendría que la hipotenusa medía
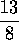, pues la proporción entre hipotenusa y cateto, que era
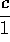, también era igual a
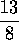y así obtendrían
.
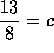Pero no obtuvieron
jamás una medida que cupiera una cantidad exacta de
veces en ambos lados del triángulo. Surgió así el primer
número irracional, aquel cuyo cuadrado es igual a 2.
Casi 2000 años después se le dioel nombre de "raíz
cuadrada de dos'' y se creó el símbolo
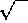para representar las raíces cuadradas. |
Se llama radicación a la operación indicada por toda
expresión matemática que consista en una potencia con
exponente racional, no entero. Se utiliza el símbolo
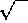, al cual se llama raíz. En los siguientes ejemplos se
observa cómo será utilizado este símbolo:
|
|
Símbolo
|
Se lee
|
|
|
raíz
cúbica de 2
|
|
|
raíz
cuarta de un medio al cubo
|
|
|
raíz
séptima de menos cinco
|
|
|
raíz
octava de siete a la menos cinco
|
|
|
raíz
quinta de menos dos tercios a la ocho
|
|
|
raíz
sexta de cinco tercios a la menos uno
|
|
|
raíz
cuadrada de cuatro quintos
|
|
| |
Toda
la expresión que se ubica dentro del símbolo de raíz
es llamada cantidad subradical, y el número que se
ubica arriba y a la izquierda de la raíz es llamado
el índice.
Por
ejemplo, en la expresión
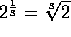se tiene Índice=3 y Cantidad subradical=2
|
|
Cuando el
índice es 2, por lo general éste se omite. Es decir,
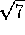significa
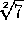y se lee "raíz cuadrada de 7''. Es importante recordar (
potenciación con base en Q y exponente
en Z ) que siempre podemos expresar una
potencia con exponente negativo como el inverso de una
potencia con exponente positivo.
Por ejemplo: |
-
-
-
-
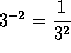
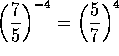(¿Por qué?)
-
-
-
-
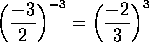
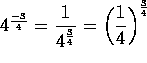(¿Por qué?)
-
|
|
En
general, dados cualesquiera números racionales a,b,m,n,
las siguientes igualdades son válidas:
|
|
|
Así,
algunos de los ejemplos anteriores se pueden escribir de
diferentes maneras:
1.
-
-
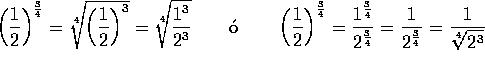
2.
-
|
|
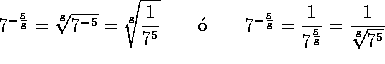
3. |
|
|
|
ó
|
|
|
|
|
|
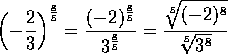
Las expresiones radicales como la del ejercicio 2 de la
interactividad anterior pueden simplificarse
transformando el exponente, que es una fracción
impropia, en suma de una fracción propia más un número
entero. Por ejemplo:
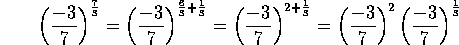
Es decir
|
|
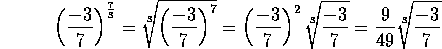
Hay muchos
casos de expresiones radicales que se pueden simplificar
hasta el punto en que la raíz desaparece; por ejemplo:
Pero como
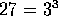, se tiene que
.
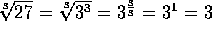en casos
como estos, se dice que se trata de una raíz exacta.
|
Ejercicio:
Encuentra 5 ejemplos de expresiones radicales que
constituyen una raíz exacta.
Obsérvese que, dada cualquier raíz
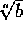se tiene que
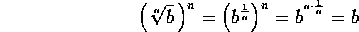
es
decir, que el número
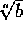multiplicado por sí mismo n veces, o elevado a la
potencia n es igual a b.
Por
eso, también se tiene que
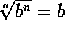, y éste es el caso de las raíces exactas que se
acaban de ver.
La
raíz n-ésima de un número no es siempre única: en el
caso de
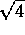, se tiene que
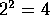y
.
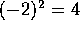es
decir, tanto 2 como -2 son raíces cuadradas de 4.
Para
evitar ambigüedad en la notación, cuando se escribe
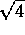se refiere a la raíz positiva de 4, y para referirse
a la raíz negativa, se escribe
:
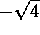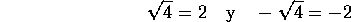
por
otra parte,
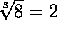, porque
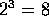, y en este caso, no se puede afirmar que -2 es
también raíz cúbica de 8, pues
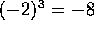. es decir,
.
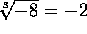Debe
observarse además que, mientras el índice de una
raíz sea un número par, la cantidad subradical debe
ser positiva para que la raíz sea un número real:
|
|
|
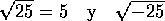
| No es
un número real, porque ningún número real
elevado al cuadrado es negativo |
|
|
Si, por otra parte, el índice es impar, la cantidad
subradical puede ser positiva o negativa, y la raíz
siempre será un número real:
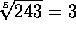y
.
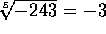Se tiene
ahora la siguiente definición:
Dado un
número racional b y un entero positivo impar n, la raíz
n-ésima de b es aquel número x que, elevado a la n-ésima
potencia, sea igual a b:
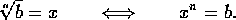
Si n es
par y b es positivo, entonces
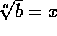, donde x>0 es tal que
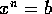. Como n es par,
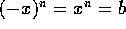y -x es llamada la n-ésima raíz negativa de b.
En
resumen, si n es par y a>0, entonces
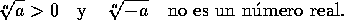
Si n es
impar y
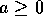, entonces
|
|
|
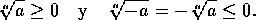
Términos Semejantes.
Se ha visto cómo
aplicar las leyes de la potenciación en el cálculo con
radicales. Estas leyes se refieren específicamente a
productos y cocientes de potencias. Pero, ¿qué se sabe
acerca de la suma y resta de potencias, que sea
aplicable a la suma y resta de radicales?
por ejemplo:
La expresión
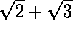¿puede simplificarse de alguna manera?
Al escribir esta suma
usando la potenciación, se obtiene:
en general, cuando se
tiene:
no puede decirse que es
igual a
.
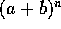por ejemplo:
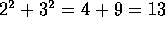y
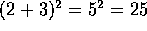
Así, en vista de que no
existe la posibilidad de igualar las expresiones:
y,
entonces simplemente se
deja la suma de radicales indicada, agrupando lo que se
llamará términos semejantes.
Cuando en una suma de
radicales aparecen términos con la misma base y el mismo
exponente, estos términos se denominarán semejantes.
Se operará con estos términos de la manera indicada en
el ejemplo siguiente:
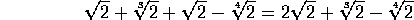
(Aquí
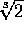y
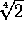no son términos semejantes a
).
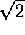Igualmente, si se tiene
la expresión
ésta puede expresase
como:
¿puedes explicar por
qué?
en general, si existen
términos semejantes en una suma de radicales, y algunos
de ellos están multiplicados por algún número real,
positivo o negativo, el cual se llama coeficiente,
se suman todos los coeficientes con su signo respectivo,
y se obtiene así el coeficiente del término resultante.
|
|
Por
ejemplo:
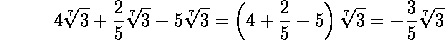
Algunas
veces es preciso hacer algunas modificaciones a las
expresiones radicales.
|
|
|
|
|
|
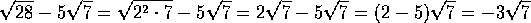
Guedj, D.
(1996). Numbers. The Universal Language. New York: Harry
N. Abrams, Inc.
Guelli, O. (1992). Contando a História da Matemática.
Sao Paulo: Editora Ática. S.A. |
|
Fundación Educativa
Héctor A. García |
