Manejo del
dinero
Interés: cuánto se paga por usar dinero (en porcentaje,
o una cantidad)
 |
El dinero no
lo prestan gratis
El dinero
siempre se puede usar para una cosa u otra, así
que hay que pagar cuando se toma dinero
prestado. |
¿Cuánto cuesta tomar
dinero prestado?
¡Se paga distinto en
distintos sitios y en momentos diferentes!
Pero normalmente
funciona así:
 |
Un porcentaje
(cada año) de la cantidad prestada
|
 |
|
Se llama
interés
|
Ejemplo:
préstamo de $1,000 en el banco
|
 |
Alex quiere
que le presten $1,000. El banco local dice "10%
de interés". Así que tomar prestados
esos $1,000 durante 1 año cuesta:
$1,000 × 10% =
$100 |
En este caso el
"interés" es $100, y la "tasa de interés" es 10% (pero
se suele decir "10% de interés" sin decir "tasa")
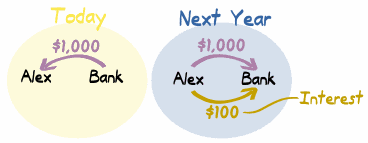
Alex tendrá que
devolver también los $1,000 originales, claro, así que
esto es lo que pasa:
 |
 |
| Alex toma
$1,000 prestado, pero tiene que devolver $1,100 |
Esta es
la idea del interés... pagar por usar dinero.
 |
Nota: aquí
el ejemplo es de un préstamo de un año completo,
pero normalmente los bancos quieren que
devuelvas un poco todos los meses, ¡y además te
cobran otros gastos! |
Nombres
Hay nombres especiales
que se usan cuando se toma dinero prestado:
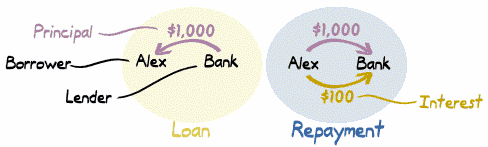
Alex es el prestatario, el banco es el
prestamista
El
principal del préstamo es $1,000
El
interés es $100
 |
Nota: la parte
importante de la palabra "interés" es inter-
que quiere decir entre (el inter-
aparece en palabras como interior e
intervalo), porque el interés ocurre entre
el principio y el final del préstamo. |
Más de un año...
¿Qué pasa si Alex
quiere que le presten dinero durante 2 años?
Interés simple
Si el banco cobra
"interés simple" entonces Alex sólo paga otro 10% el año
siguiente.

Alex paga un interés de ($1,000 × 10%) x 2 años = $200
Así funciona el interés
simple... se paga la misma cantidad de interés todos los
años.
Ejemplo: si a Alex le
prestaran el dinero durante 5 años, el cálculo sería
así:
• Interés = $1,000 × 10% x 5 años = $500
• Más el principal de $1,000, Alex tiene que pagar
$1,500 después de 5 años
Interés compuesto
Pero un banco podría
decir "si me pagaras todo al año, y luego te lo
prestara... ¡te estaría prestando $1,100 para el
segundo año!"
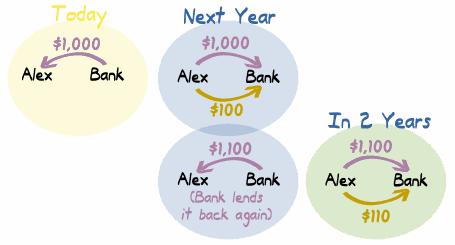
Y Alex
pagaría $110 de interés el segundo año, no sólo
$100.
Esto
es porque Alex está pagando 10% de $1,100 no sólo de
$1,000
Te puede parecer injusto... pero imagina
que TÚ eres el que le presta dinero a Alex. Después de
un año pensarías: "Ahora Alex
me debe $1,100, y todavía está usando mi dinero, ¡yo
tendría que recibir más interés!"
Y esta es la manera
normal de calcular intereses. Se llama compuesto.
En el interés
compuesto primero calculas el interés del primer
periodo, lo sumas al total, y después calcula el
interés del siguiente periodo, y sigue... así:
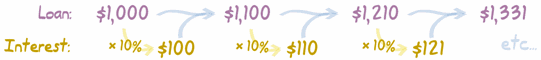
Si lo piensas... es
como pagar interés por el interés. Porque si después de
un año Alex debe $100 de interés, el banco lo considera
otro préstamo y cobra interés por él.
Después de unos años
puede aumentar muchísimo. Esto es lo que pasa con un
préstamo de 5 años:
|
Año
|
Préstamo
inicial
|
Interés
|
Préstamo
final
|
|
0 (Ahora)
|
$1,000.00
|
($1,000.00 × 10% = )
$100.00
|
$1,100.00
|
|
1
|
$1,100.00
|
($1,100.00 × 10% = )
$110.00
|
$1,210.00
|
|
2
|
$1,210.00
|
($1,210.00 × 10% = )
$121.00
|
$1,331.00
|
|
3
|
$1,331.00
|
($1,331.00 × 10% = )
$133.10
|
$1,464.10
|
|
4
|
$1,464.10
|
($1,464.10 × 10% = )
$146.41
|
$1,610.51
|
|
5
|
$1,610.51
|
|
|
Así que después de 5 años Alex tendría que devolver
$1,610.51
Y el
interés del último año es $146.41 ... ¡mira qué rápido
crece!
(Compáralo con el interés simple de $100 al año)
¿Qué es el año 0?
El año 0 es el
año que empieza cuando "nace" el préstamo, y termina
justo antes del primer cumpleaños. Así que el principio
del año 1 es el "primer cumpleaños".
Así vemos que el
principio del año 5 es exactamente cuando el
préstamo cumple 5 años.
|
En resumen:
Para calcular el
interés compuesto, calcula el interés del primer
periodo, súmalo, calcula el interés del
siguiente periodo, etc.
(Hay maneras
más rápidas, te las explicamos en Interés
compuesto) |
¿Porqué tomar
prestado?
Bueno... a veces uno
quiere comprar alguna cosa. Pero ya has visto que te
puede salir muy caro pagar el préstamo.
Pero si tienes un
negocio puedes usar el dinero para ganar todavía más
dinero.
 |
Ejemplo:
negocio de pollos
Te prestan
$1,000 para abrir un negocio de pollos (comprar
polluelos, comida para pollos y cosas así).
Un año después
vendes las gallinas por $1,200.
Devuelves
$1,100 al banco (los $1,000 originales más 10%
de interés) y te quedan $100 de beneficios.
¡Y has usado el
dinero de otro para eso!
Pero...
recuerda. ¿Qué pasaría si sólo los vendieras por
$800? ... Todavía tendrías que devolver al banco
$1,100 así que tendrías
una pérdida de $300. |
Inversión
¡El interés compuesto
puede funcionar a tu favor!
Una inversión es
cuando pones dinero en un sitio donde puede crecer,
como un banco o un negocio.
Si inviertes dinero con
una buena tasa de interés, puede crecer muy bien.
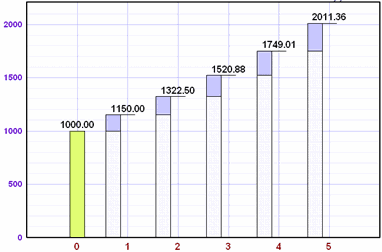
Esto es lo que hace un
15% de interés sobre $1,000:
|
Año
|
Préstamo
inicial
|
Interés
|
Préstamo
final
|
|
0 (Ahora)
|
$1,000.00
|
($1,000.00 × 15% = )
$150.00
|
$1,150.00
|
|
1
|
$1,150.00
|
($1,150.00 × 15% = )
$172.50
|
$1,322.50
|
|
2
|
$1,322.50
|
($1,322.50 × 15% = )
$198.38
|
$1,520.88
|
|
3
|
$1,520.88
|
($1,520.88 × 15% = )
$228.13
|
$1,749.01
|
|
4
|
$1,749.01
|
($1,749.01 × 15% = )
$262.35
|
$2,011.36
|
|
5
|
$2,011.36
|
|
|
¡Se dobla y más todavía en sólo 5 años!
Claro que tendrías
suerte si encuentras una inversión segura al 15% ...
pero ya ves el poder del interés compuesto. El
gráfico de tu inversión sería así:
A lo mejor no tienes
$1,000, pero si pudieras ahorrar $200 cada año durante
10 años al 10% de interés, tu dinero crecería así:
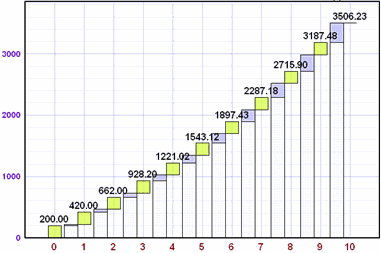
¡$3,506.23
después de 10 años!
Por 10 años de $200 cada uno.
Menos de un año...
El interés no siempre
se cobra anualmente. Puede ser semianual (cada 6 meses),
mensual, ¡hasta diario!
Pero se aplican las
mismas reglas:
- Si es interés
simple, sólo hay que calcular el interés de un
periodo y multiplicar por el número de periodos.
- Si es interés
compuesto, calcula el interés del primer periodo,
súmalo y calcula el interés del siguiente, etc.
|