L a G r a n E n c i c l o p e d i a I l u s t r a d a d e l P r o y e c t o S a l ó n H o g a r
![]()
- Ejemplo: Averiguar el m.c.m. de
Sacar el M.C.D. de 20 y 10:
20: 20, 40, 60, 80... 10: 10, 20, 30...
20 es el múltiplo menor que es común a ambos números.
Multiplos: los múltiplos de un número se obtienen multiplicando dicho número por los números naturales 0, 1, 2, 3, 4, 5.....
Ejemplo: múltiplos del 7: 7x0=0; 7x1=7; 7x2=14; 7x3=21; 7x4=28; 7x5=35 ....
O sea son múltiplos del 7:, 0, 7, 14, 21, 28, 35, 42, 48, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168...
Ejemplo: Calcular el m. c. m. de 4, 5 y 6.
Se hace la descomposición de factores (que ya la explicamos en el máximo común divisor). Lo hacemos de la siguiente forma:
4= 2x2
5= 5
6= 2x3
Se toman los factores comunes y no
comunes con el mayor exponente y se multiplican: 2x2 x3 x5 = 60. El
mcm de 4,5 y 6 es 60.
Mínimo común múltiplo de dos o más números:
El
mínimo común múltiplo de dos números es
el más pequeño de los múltiplos comunes a ambos.
|
El más pequeño de estos múltiplos comunes es el número 6, entonces se dice que 6 es el mínimo común múltiplo de 2 y 3, y lo escribimos así: m.c.m. (2 y 3) = 6.
Existe una manera mas práctica y fácil para hallar el m.c.m, sobre todo si se trata de números muy altos.
Consiste en descomponer cada número en factores primos y el mínimo común múltiplo será igual al producto de los factores comunes y no comunes con su mayor exponente.
Para descomponer un número en sus factores primos se sigue el siguiente procedimiento
Se divide el número entre el número primo más pequeño que lo divida exactamente.
Se divide el cociente de la división anterior entre el siguiente número primo que dé división exacta.
Se continúan efectuando cálculos hasta llegar a un cociente igual a uno.
El número que se descompuso en sus factores primos dede ser igual al producto de todos los divisores resultantes.
Procedemos a descomponer al número 60
60 es divisible por varios números primos (o factores primos): 2, 3, 5
Tomemos el factor primo 2 para usarlo como divisor de 60.
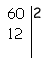 El resultado es 12, como 12 se puede seguir dividiendo... |

Observa que 60 se descompone en sus factores primos de la siguiente manera:
60 = 2 x 2 x 3 x 5 => 60 = 2 x 3 x 5
Ahora se continua la división del residuo que se obtuvo, el 12, por el siguiente factor primo que corresponde, el 3. Observa el residuo es 4 y 4 puede ser de nuevo divisible, se divide entre 2 hasta llegar a un número que no admita mas divisores.
Observa otro ejemplo:
Calcular el mínimo común múltiplo entre los números 2, 5 y 10.
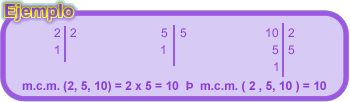
Observa
el siguiente:

Máximo común divisor de dos o más números
Para hallar el máximo común divisor (m.c.d.) de varios números, se procede de la misma manera que para el m.c.m., con la diferencia de que luego de descomponer las cantidades dadas en sus factores primos, se toman de ellos, el producto de los factores comunes con su menor exponente.