Adición y
sustracción
Te invitamos a ponerte los
anteojos del razonamiento y los guantes de la
lógica, a tomar el lápiz como bisturí para
convertirte en cirujano matemático.
¡Vas a sacar cálculos!
La palabra
cálculo
tiene su origen en el latín "calculus" que
significa piedra, elemento de la naturaleza que
antiguamente se usó para contar.
De esta
sencilla palabra se derivan muchos términos como
calculista, calculable y también, nuestra
querida amiga, la calculadora. Entremos en
materia y revisemos cada operación dentro del
conjunto de los números cardinales.
LAS
PROPIEDADES DE LA SUMA
Si observamos la suma:
10 + 13 + 8 + 17 = 48
Sumandos Total de la suma
1) Propiedad Conmutativa: El orden de los sumandos no
altera el total de la suma
Ejemplo:
•10 + 13 + 8 + 17 = 48
•13 + 10 + 17 + 8 = 48
1) Propiedad asociativa: Si agrupamos los sumandos de
distinta forma el resultado final de la suma siempre es
el mismo.
Ejemplo:
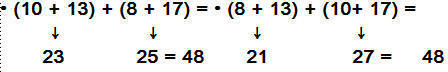
2) Propiedad del Cero: Si sumamos 0 a cualquier
número el resultado es el mismo número.
Ejemplo: •25 + 0 =25 • 0 + 25 = 25
PRACTICA
Identifica la propiedad de la suma que se
utiliza en cada caso:
1) 120 + (1,110 + 500) = (120 + 1,100) + 500
_______________________________
2) 13 + 24 + 36 = 24 + 36 + 13
__________________________________________
3) 0 + 50 = 50
________________________________________________________
4) 88 + 25 + 12 + 77 = 25 + 77 + 12 + 88
___________________________________
5) (3 + 2) + 6 = (6 + 3) +
2_______________________________________________
6) 36 + 0 =
36_________________________________________________________
Sumar
decimales
Sumar
decimales es fácil si lo haces ordenadamente
Para sumar
decimales sigue estos pasos:
-
Escribe los números, uno
bajo el otro, con los puntos
decimales alineados.
-
Añade
ceros para que los números
tengan la misma longitud.
-
Suma
normalmente, y recuerda
poner el punto decimal en la
respuesta.
Ejemplo: suma 1.452 y 1.3
|
Alinea los decimales: |
|
|
1.452 |
|
|
|
+ |
1.3 |
|
|
|
|
|
|
"Rellena"
con ceros: |
|
|
1.452 |
|
|
|
+ |
1.300 |
|
|
|
|
|
|
Suma: |
|
|
1.452 |
|
|
|
+ |
1.300 |
| |
|
|
|
|
|
|
|
2.752 |
Ejemplo: suma 3.25, 0.075 y
5
|
Alinea los
decimales: |
|
|
3.25 |
|
|
|
|
0.075 |
|
|
|
+ |
5. |
|
|
|
|
|
|
"Rellena " con
ceros: |
|
|
3.250 |
|
|
|
|
0.075 |
|
|
|
+ |
5.000 |
|
|
|
|
|
|
Suma: |
|
|
3.250 |
|
|
|
|
0.075 |
|
|
|
+ |
5.000 |
| |
|
|
|
|
|
|
|
8.325 |
|
|
Adición
Términos como
juntar, agregar, buscar totales, son
claves para aplicar esta importante operación
matemática. En ella distinguimos: los
sumandos,
que son numerales separados por el signo
más (+), y la
suma, que es el
resultado de la operación:
12O +
140 +
200 =
460
Un dato curioso de la
adición, es la suma que se obtiene de números
pares e
impares:
8 +
2 =
10
7 +
3 =
10
¿Y cuándo la suma es
impar?
Observa:
pares e
impares:
9 +
8 =
15
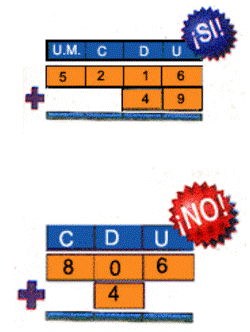
Cuando aplicas la adición
en forma vertical, debes hacer coincidir las
columnas de posición de todos los sumandos.
Recuerda que en cada columna las cifras tienen
diferente valor:
Resolvamos el
siguiente ejemplo:
375 560 + 28 481
En forma vertical
quedaría:
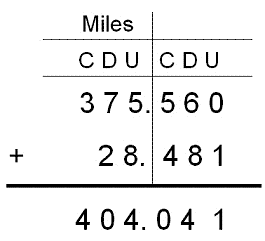
Partiremos sumando primero
las unidades: 0 U + 1 U = 1 U,
por lo que pondremos un 1 bajo las unidades.
Luego sumaremos las decenas: 6
D + 8 D = 14 D = 1 C + 4 D, por lo que dejaremos
un 4 bajo las decenas y reservaremos 1 centena.
Seguiremos sumando las centenas:
5 C + 4 C = 9 C + 1 C que habíamos reservado es
igual a 10 C = 1 UM + 0 C, por lo que pondremos
un 0 bajo las centenas y reservaremos 1 UM.
Continuamos entonces con unidades de mil:
5 UM + 8 UM = 13 UM + 1 UM que habíamos
reservado es igual a 14 UM = 1 DM + 4 UM, por lo
dejaremos un 4 bajo las UM y reservaremos 1 DM.
Sumaremos ahora las decenas de mil:
7 DM + 2 DM = 9 DM + 1 DM que habíamos reservado
es igual a 10 DM = 1 CM + 0 DM, dejaremos
entonces un 0 bajo las decenas de mil y
reservaremos 1 CM.
Y por último sumaremos las centenas de
mil: 3 CM + 0 CM = 3 CM + 1 CM que
habíamos reservado es igual a 4 CM, pondremos
entonces un 4 bajo las CM, lo que nos da una
suma de 404 041.
SUMAR
NÚMEROS CARDINALES
Sumamos cuando tenemos varias cantidades y
queremos conocer el total de las mismas
Ejemplo: En un almacén hay 14,567 lápices rojos
y 7,671 lápices azules. ¿Cuánto lápices hay en
total?
Para conocer la cantidad total de lápices
debemos sumar
14,567 + 7,671 =
• 14,567
+ 7,671
8 Se suman las unidades y se
reagrupa si es necesario.
ǀ
ǀ
• 14,567
+ 7,671
238 Se suman las decenas y las
centenas y se reagrupa si fuera necesario.
ǀ
ǀ
ǀ
• 14,567
+ 7,671
2 238 Se suman las unidades de
millar y se reagrupa si fuera necesario.
ǀ
ǀ
ǀ
•
1 4,567
+ 7,671
22,238 Se suman las decenas de millar.
PRACTICA
Realiza las siguientes sumas:
Viste que fácil es
sumar!!!
Sustracción
¡Cuántas veces decimos:
me queda, me falta, la diferencia...!
Ahí nos referimos a la sustracción, una
operación que tiene como elementos:
16 -
7 = 9
MINUENDO -
SUSTRAENDO = RESTA
O DIFERENCIA
La sustracción no es
cerrada, porque no siempre tiene solución en los
números cardinales:
3 -
12 = ?
Sólo se puede resolver
cuando el minuendo es mayor o
igual que el sustraendo.
Tenemos la siguiente
sustracción: 12 - 3 = 9. Pero, ¿por qué es 9?
Porque 9 + 3 = 12.
Entonces, la
sustracción es la operación inversa a la adición.
Por eso, para comprobar si la diferencia está
correcta, sumamos la resta, más el sustraendo y
debemos obtener el minuendo.
Veamos el
siguiente ejemplo:
425 - 55 = 370
Si esta sustracción es
correcta, debe darse lo siguiente:
370 + 55 = 425
Como la suma es correcta,
entonces el resultado de la sustracción también
es correcto.
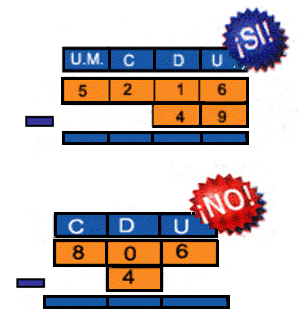
Cuando aplicas la
sustracción en forma vertical, debes hacer
coincidir las columnas de posición del minuendo
y el sustraendo. Recuerda que en cada columna
las cifras tienen diferente valor:
Resolvamos el
siguiente ejemplo:
425,672 - 15,392
En forma vertical
quedaría:

Partiremos restando
primero las unidades: 2 U - 2 U
= 0 U, por lo que pondremos un 0 bajo las
unidades.
Luego seguiremos con las decenas:
7 D - 9 D, como esto no lo podemos resolver, le
pediremos prestada 1 C a las 6 C, por lo que nos
quedaría ahora 17 D - 9 D = 8 D, por lo que
pondremos un 8 bajo las decenas.
Seguimos entonces con las centenas:
5 C (6 C - 1 C, recuerda que le prestamos una C
a las 7 D) - 3 C = 2 C, por lo que pondremos un
2 bajo las centenas.
Continuamos con las unidades de mil:
5 UM - 5 UM = 0 UM, por lo que pondremos un 0
bajo las unidades de mil.
Restaremos ahora las decenas de mil:
2 DM - 1 DM = 1 DM, por lo que pondremos un 1
bajo las decenas de mil.
Y por último restamos las centenas de
mil: 4 CM - 0 CM = 4 CM, por lo que
pondremos un 4 bajo las centenas de mil.
Finalmente el resultado de esta resta es 410
280.
Viste lo fácil que es
restar, sigue prácticando...
Restar
decimales
Restar
decimales es fácil si lo haces
ordenadamente
Para
restar decimales sigue estos
pasos:
-
Escribe los dos números, uno
bajo el otro, con los puntos
decimales alineados.
-
Añade
ceros para que los números
tengan la misma longitud.
-
Suma
normalmente, y recuerda
poner el punto decimal en la
respuesta.
Ejemplo: resta 0.03 de 1.1
|
Alinea los decimales: |
|
|
1.1 |
|
|
|
- |
0.03 |
|
|
|
|
|
|
"Rellena"
con ceros: |
|
|
1.10 |
|
|
|
- |
0.03 |
|
|
|
|
|
|
Resta: |
|
|
1.10 |
|
|
|
- |
0.03 |
| |
|
|
|
|
|
|
|
1.07 |
Así que era lo mismo que 110
- 3 = 107, pero poniendo
puntos decimales
Ejemplo: calcula 7.005-0.55
|
Alinea los
decimales: |
|
|
7.005 |
|
|
|
- |
0.55 |
|
|
|
|
|
|
"Rellena" con
ceros: |
|
|
7.005 |
|
|
|
- |
0.550 |
|
|
|
|
|
|
Resta: |
|
|
7.005 |
|
|
|
- |
0.550 |
| |
|
|
|
|
|
|
|
6.455 |
Y
esta era igual que 7,005
- 550 = 6,455
PRÁCTICA DE SUMA Y RESTA
DE NÚMEROS DECIMALES:
• Halla las sumas o
restas según
correspondan, realízalos
copiando las cantidades
de forma vertical:
1) 32.85 + 2.003=
2)
13.21
—7.06
3) 68.29 + 90.21
4) 26.004 —11.013
_______________
_______________
_____________
________________
_______________
_______________
_____________
________________
+______________
—_____________
+____________
—______________
_______________
_______________
______________
________________
5) En un salón de clase
de 6to. Grado se
obtuvieron las
siguientes puntaciones
Grupo A
Grupo
B
María
20.146
Jorge 20.116
Juan
20.175
Berta 20.245
Pedro
20.257
Margarita 26.187
Elena
25.476
José 18.237
Halla:
a) La diferencia entre
la puntuación mayor y la
menor del Grupo A
b) La diferencia entre
la puntuación mayor y la
menor del Grupo B
c) El total de
puntuación obtenido por
el Grupo A
d) El total de
puntuación obtenida por
el Grupo B
c) La diferencia entre
los totales de puntación
obtenidas por el Grupo A
y los totales de
puntuación obtenidas por
el Grupo B.
RESTAR NÚMEROS
CARDINALES
Restamos
si
tenemos dos cantidades y
queremos saber cuánto
una cantidad
es mayor
de la otra.
En el almacén teníamos
14,567 lápices rojos y
7,671 lápices azules.
¿Cuánto mayor es la
cantidad de lápices rojo
que de lápices azules?
Para conocer la
diferencia entre los
lápices debemos restar
14,567 — 7,671=
• 14,567
— 7,671
6
Se restan las unidades y
se reagrupa si es
necesario.
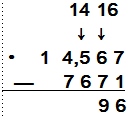 Se restan las
decenas y se reagrupa si
es necesario. Se restan las
decenas y se reagrupa si
es necesario.
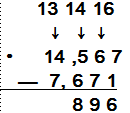 Se restan las
centenas y se reagrupa
si es necesario. Se restan las
centenas y se reagrupa
si es necesario.
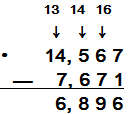 Se restan las
unidades y decenas de
millar
Se restan las
unidades y decenas de
millar
PRACTICA
Realiza las siguientes
rectas:
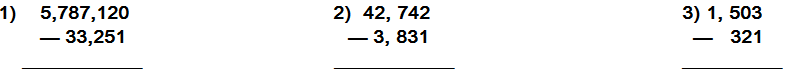
ESTIMAR
SUMAS Y RESTAS DE
NUMEROS CARDINALES
Cuando
queremos
conocer
el valor
aproximado de varias
cantidades podemos
estimar la misma
Ejemplos:
1) Estima: 2,788 +
4,125.
•
2,788
+
4,125 Observa
el primer dígito de cada
número.
•
2,788
+
4,125
Observa el número que
está a su derecha.
•
3,000
Si el número de la
derecha es mayor o igual
que 5 se le suma 1 al
1er. dígito
+ 4,000
Si el número de la
derecha es menor que 5
el 1er. dígito se queda
igual y en todos
en
todos los casos los
dígitos de la derecha se
cambian por ceros.
• 3,000
+4,000
7,000 Se suma.
2) Estima 5,125 - 3,587
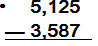
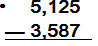 |
Observa el
primer dígito de
cada número
|
|
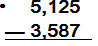 |
Observa el
número que está
a su derecha.
|
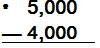 |
Como el dígito
de la derecha es
menor que 5 se
queda igual
Como dígito de
la derecha es
mayor que 5 se
aumenta un
digito al primer
número
(3+1) y en los
dos casos los
dígitos que
están a la
derecha se
cambian por
cero. |
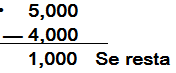
PRACTICA
1) Estima:
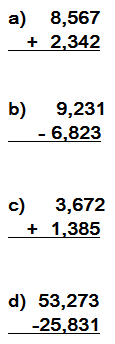
ESTIMAR SUMAS Y RESTAS
DE NUMEROS DECIMALES
Cuando
queremos
conocer
el valor
aproximado de varias
cantidades podemos
estimar la misma.
Ejemplos:
1) Estima 2.5 + 0.7 +
3.19
•
2.5
0.7
+
3.19
Observa el primer
dígito de cada número.
•
2.5
0.7
+ 3.19
Observa el número que
está a su derecha.
•
3 Si el número de
la derecha es mayor o
igual que 5 se le suma 1
al mismo.
1 Si el número
es mayor o igual que 5
se le suma 1 al mismo.
+ 3
Si el número de la
derecha es menor que 5
se queda igual y en
todos los casos se
eliminan
los dígitos a la
derecha.
•
3
1
+ 3
7 Se suma.
2) Estima 5.17 — 0.6
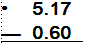 |
Observa el
primer dígito de
cada número.
|
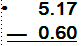 |
Observa
el número que
está a su
derecha.
|
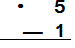 |
Como el
dígito de la
derecha es menor
que 5 se queda
igual.
Como dígito de
la derecha es
mayor que 5 se
aumenta un
digito (0 + 1)
y en todo los
casos se
eliminan los
dígitos a la
derecha. |
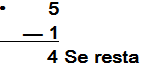
PRACTICA
1) Estima:
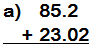
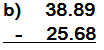
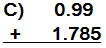
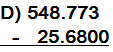

[TOMAR EL EXAMEN DE ESTE
CAPITULO]
Es un examen de 20
preguntas, pero cada vez
que lo tomes será
diferente.
|
|