|
![]()
Los números como fracciones

Cuando asistes a un cumpleaños habrás notado que a la hora de repartir el bizcocho comienzan las madres a contar cuántas personas se encuentran en la fiesta, de manera que la torta alcance para todos y los pedazos sean más o menos del mismo tamaño.
Expresar esto en números es muy fácil. el bizcocho representa la unidad (un bizcocho); las personas invitadas a la fiesta (8,10,15...) representan las partes o porciones iguales en que el bizcocho (la unidad) deberá ser dividida. Por lo tanto si los invitados a la fiesta son 8, lel bizcocho deberá dividirse en 8 partes iguales y a cada invitado le corresponderá UN OCTAVO del bizcocho entero

Si uno de los invitados no come bizcocho, habrá un afortunado al que le tocarán dos porciones, es decir dos pedazos de los 8 en que se dividió el bizcocho; esto es DOS OCTAVOS de bizcocho.

- El número colocado bajo la línea de fracción indica en cuántas partes ha sido dividida la unidad. Éste recibe el nombre de DENOMINADOR.
- El número que se encuentra sobre la línea de fracción indica las partes que se están seleccionando de las que ya se dividieron. A este número se le da el nombre de NUMERADOR.
|
En la
siguiente fracción el:
|
|
*Numerador es 1 y el *Denominador es el 8 |
|
1
8 |
=
|
1/8
|
Una fracción, en general, es la
expresión de una cantidad dividida por otra, y una
fracción propia representa las
partes que tomamos de un todo.
El ejemplo clásico es el de un queso que partimos en
porciones.
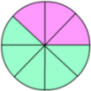
En el dibujo, hemos hecho 8 porciones, 3 rosas y 5
verdes.
| Si tomamos las 3 rosas, representan 3 porciones de las ocho en las que hemos dividido el queso, es decir 3 / 8 del queso, y si tomamos las 5 verdes, representan 5 porciones de las ocho en las que hemos dividido el queso, es decir 5 / 8 del queso. |
 |
Las partes que tomamos ( 3 - 5 ) se llaman numerador y las partes en que dividimos el queso ( 8 ) denominador.
CLASIFICACIÓN DE LAS FRACCIONES
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.
| Tipo | Características | Ejemplos |
| Propia | El numerador es menor que el denominador | 1 / 2, 7 / 9 |
| Impropia | El numerador es mayor que el denominador | 4 / 3, 5 / 2 |
| Homogéneas | Tienen el mismo denominador | 2 / 5, 4 / 5 |
| Heterogéneas | Tienen distinto denominador | 3 / 7, 2 / 8 |
| Entera | El numerador es igual al denominador; representan un entero | 6 / 6 = 1 |
| Equivalentes | Cuando tienen el
mismo valor. Dos fracciones son
equivalentes si son iguales sus productos cruzados |
2/3 y 4/6 2x6 = 3x4 |
Si en una fracción multiplicamos o dividimos el numerador y el denominador por un mismo numero, obtenemos una fracción equivalente a la primera, pues ambas tienen el mismo valor. Por ejemplo:
| 1 | (1 x 4) | 4 | 3 | (3 : 3) | 1 | |||||||||
| — | = | ——— | = | — | = | 0,5 ; | — | = | ——— | = | — | = | 0,2 | |
| 2 | (2 x 4) | 8 | 15 | (15 : 3) | 5 |
Simplificar o Reducir una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, dividimos el numerador y el denominador por los factores comunes a ambos.
SUMA Y RESTA DE FRACCIONES
Si las fracciones tienen el mismo denominador (homogéneas), se suman o restan los numeradores y se pone el mismo denominador.
Ejemplo:
| 3 | 2 | (3 + 2) | 5 | 5 | 2 | (5 – 2) | 3 | |||||||
| — | + | — | = | ——— | = | — ; | — | – | — | = | ——— | = | — | |
| 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 |
Si las fracciones tienen distinto denominador (heterogéneas), lo primero que tenemos que hacer es igualar los denominadores. Para conseguirlo, buscamos dos fracciones equivalentes a las dadas, multiplicando el numerador y el denominador de cada una de ellas por el denominador de la otra. Una vez obtenido el mismo denominador, procedemos como en el caso anterior, sumamos los numeradores y ponemos el denominador común.
Ejemplo:
| 2 | 3 | (2 x 7) | (3 x 5) | 14 | 15 | 29 | ||||||
| — | + | — | = | ——— | + | ——— | = | —— | + | —— | = | —— |
| 5 | 7 | (5 x 7) | (7 x 5) | 35 | 35 | 35 |
MULTIPLICACIÓN DE FRACCIONES
El producto de varias fracciones es igual a otra fracción que tiene por numerador el producto de los numeradores y por denominador el producto de los denominadores.
Ejemplo:
| 3 | 4 | 2 | (3 x 4 x 2) | 24 | 2 | ||||||
| — | x | — | x | — | = | ———— | = | —— | simplificando | = | — |
| 4 | 5 | 3 | (4 x 5 x 3) | 60 | 5 |
FRACCIÓN DE UN NÚMERO
Calcular la fracción de un número es lo mismo que multiplicar la fracción por ese número.
Ejemplo: Calcular los 2 / 3 de 60 :
| 2 | 2 | (2 x 60) | 120 | |||||||||
| — | de | 60 | = | — | x | 60 | = | ——— | = | —— | = | 40 |
| 3 | 3 | 3 | 3 |
DIVISIÓN DE FRACCIONES
El cociente de dos fracciones es otra fracción que tiene por numerador el producto del numerador de la primera por el denominador de la segunda, y por denominador el producto del denominador de la primera por el numerador de la segunda.
Ejemplo:
| 4 | 3 | (4 x 5) | 20 | |||
| — | : | — | = | ——— | = | —— |
| 9 | 5 | (9 x 3) | 27 |
WWW.PROYECTOSALONHOGAR.COM