Radicals - Rational and irrational numbers: Level 2
The definition of the square root radical
Example 3. Solve for x:
| (x + 3)² | = | 5 | |
| Solution. This has the form | |||
| z² | = | a. | |
| Therefore we solve it in the same manner as Example 2. | |||
| x + 3 | = | ± |
|
| x | = | −3 ± |
|
Problem 6. Solve for x.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | (x − 1)² | = | 2 | b) | (x + 5)² | = | 6 | |
| x − 1 | = | ± |
x + 5 | = | ± |
|||
| x | = | 1 ± |
x | = | −5 ± |
| c) | (x − p)² | = | q + r |
| x − p | = | ± |
|
| x | = | p ± |
|
The definition of the square root radical
Here is the formal rule that implicitly defines the symbol ![]() :
:
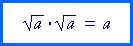
A square root radical multiplied by itself
produces the radicand.
| Examples. | = | 2 | |
| (3a | = | 3²a²( |
|
| = | 9a²· 10 | ||
| = | 90a². | ||
Problem 7. Evaluate the following.
| a) | b) | ||||||
| c) | ( |
d) | |||||
| e) | (5 |
f) | (a4 |
||||
Example 4. Multiply out ![]()
![]() (
(![]() +
+ ![]() ). That is, distribute
). That is, distribute ![]()
![]() .
.
| Solution. | = | ||
| = | 2 |
||
Problem 8. Following the previous Example, multiply out
![]()
![]() (
(![]() +
+ ![]() ).
).
| = | ||
| = | ||
Rationalizing a denominator
Rationalizing a denominator is a simple technique for changing an irrational denominator into a rational one. We simply multiply the radical by itself -- but then we must multiply the numerator by the same number.
| Example 5. Rationalize this denominator: | 1 |
Solution. Multiply both the numerator and denominator by ![]() :
:
![]()
The denominator is now rational.
2 |
can also take the form ½ |
2 |
= ½ |
| For, any fraction | a b |
can be written as the numerator times the |
reciprocal of the denominator.
| Problem 10. Rationalize the denominator: | 2 |
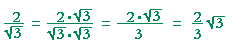
Problem 11. Show each of the following by transforming the left-hand side.
| a) | 6 |
= | 2 |
6 |
= | 3 |
= | 2 |
| b) | 9 |
= | 2 |
9 |
= | 6 |
= | 2 |
| c) | = | ab |
= | b |
Real numbers
A real number is any number that you would expect to find on the number line. The absolute value of each real number names a distance from 0.
![]()
The two main categories of real numbers are rational and irrational. These numbers are the subject of calculus and of scientific measurement.
A real variable is a variable that takes on real values.
Problem 12. Let x be a real variable, and let 3 < x < 4. Name five values that x might have.
For example, 3.1, 3.14, ![]() ,
, ![]() ,
, ![]() .
.
Problem 13. If the square root is to be a real number, then the radicand may not be negative. (There is no such real number, for example, as ![]() .)
.)
If ![]() is to be real, then we must have x ≥ 0.
is to be real, then we must have x ≥ 0.
(If you are not viewing this page with Internet Explorer 6, then your browser may not be able to display the symbol ≥, "is greater than or equal to;" or ≤, "is less than or equal to.")
Therefore, what values are permitted to the real variable x ?
a) ![]() x − 3 ≥ 0; that is, x ≥ 3.
x − 3 ≥ 0; that is, x ≥ 3.
b) ![]() 1 + x ≥ 0; x ≥ −1.
1 + x ≥ 0; x ≥ −1.
c) ![]() 1 − x ≥ 0; −x ≥ −1, which implies x ≤ 1.
1 − x ≥ 0; −x ≥ −1, which implies x ≤ 1.
d) ![]() x² ≥ 0. In this case, x may be any real number.
x² ≥ 0. In this case, x may be any real number.
Next Lesson: Simplifying radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com