31
RECTANGULAR COORDINATES
Actual versus potential infinities
WE WILL BEGIN with vocabulary.
First, a coordinate. A coordinate is a number. It labels a point on a line.
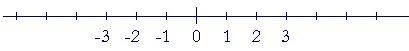
The coordinate 0 is called the origin of coordinates. Points to the right of 0 are labeled with positive numbers: 1, 2, 3, etc. Points to the left of the origin are labeled with negative numbers: −1, −2, −3, etc. . Those coordinates are the "addresses" of those points.
A coordinate axis is a line with coordinates.
Now, to label the points in a plane, we will need more than one coordinate axis, and we place a second at right angles to the first.

Points above the origin have positive coordinates; points below have negative coordinates.
Those lines are called rectangular coordinate axes; the coordinates on them are called rectangular coordinates. They are also called Cartesian coordinates, after the 17th century philosopher and mathematician René Descartes; for he was one of the first to exploit the geometrical possibilities of coordinates.
The rectangular coordinates of a point are an ordered pair, (x, y).
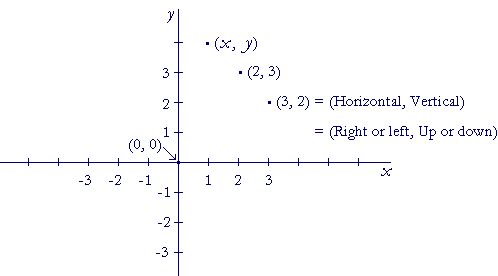
The pair (2, 3) -- over 2 and up 3 -- labels a different point than (3, 2): over 3 and up 2. The horizontal coordinate -- Right or left -- is always entered first. The vertical coordinate -- Up or down -- is always entered second. For that reason, (2, 3) is called an ordered pair.
The coordinates of the origin are (0, 0). We don't move right or left and we don't move up or down. We will see that 0 is an extremely important coordinate. It means that the point is on one of the axes.
Now the horizontal axis is always called the x-axis, and the vertical axis is always called the y-axis. The first coordinate, then, is called the x-coordinate; the second is called the y-coordinate. We always write (x, y).
Finally, the coordinate axes divide the plane into four quadrants:

The first, the second, the third, and the fourth. The quadrants are labeled counter-clockwise.
Problem 1. Name the coordinates of each point.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) |  |
b) | 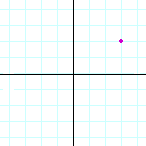 |
c) | 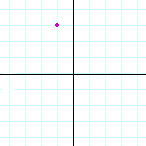 |
||||||||
| (2, 3) | (3, 2) | (−1, 3) | |||||||||||
| d) | 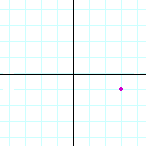 |
e) | 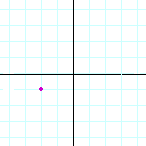 |
f) |  |
||||||||
| (3, −1) | (−2, −1) | (0, 3) | |||||||||||
| g) | 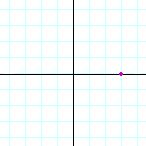 |
h) |  |
i) | 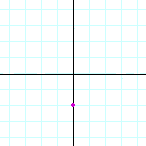 |
||||||||
| (3, 0) | (−2, 0) | (0, −2) | |||||||||||
Problem 2. Coordinate 0.
a) On the x-axis, what is the value of every y-coordinate? 0

On the x-axis, we don't move up or down. At every point, y = 0.
b) On the y-axis, what is the value of every x-coordinate? 0
On the y-axis, we don't move right or left. At every point, x = 0.
c) Where is the y-coordinate always 0? On the x-axis.
d) Where is the x-coordinate always 0? On the y-axis.
Problem 3.
a) Where is the x-coordinate always 2?
On the vertical line 2 units to the right of the origin.
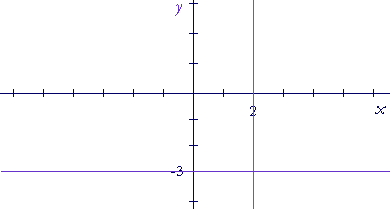
b) Where is the y-coordinate always −3?
On the horizontal line 3 units below the origin.
Problem 4. In which quadrant does each point lie? Or is it on an axis; if so, which axis?
| a) | (2, −3) Fourth | b) | (−4, 2) Second | |
| c) | (0, −5) On the y-axis. | d) | (−3, −1) Third | |
| e) | (5, 0) On the x-axis. | f) | (−6, 9) Second | |
| g) | (0, −4) On the y-axis. | h) | (−4, 0) On the x-axis. | |
| i) | (−1, −1) Third | j) | (0, 6) On the y-axis. | |
| k) | (−1, 0) On the x-axis. | l) | (0, 1) On the y-axis. | |
| m) | (5, −2) Fourth | n) | (−5, 0) On the x-axis. | |
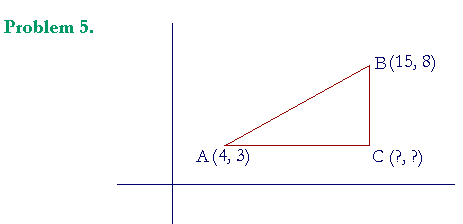
The extremities of a straight line AB have coordinates (4, 3) and (15, 8), and that line is the hypotenuse of a right triangle ABC. Name the coordinates of the right angle at C.
C has the same x-coordinate as B. Therefore its x-coordinate is 15. And C has the same y-coordinate as A. Therefore its y-coordinate is 3. Its coordinates are (15, 3).
Actual versus potential infinities
The concept of an actually infinite straight line, is that it has no extremities
-- no end points.
![]()
We are to imagine that such a line actually exists. Now.
A potentially infinite straight line, on the other hand, has two extremities.
![]()
It is potentially infinite in the sense that it may be extended in either direction for as far as we please. It is a line that we could actually draw.
The student should be warned that when writers use the expression "straight line" these days, they invariably mean an actually infinite line. Hence, they refer to any finite line, with its two extremities, as a line segment. They imagine that every finite straight line is a segment of an actually infinite one. This has become the standard modern point of view. In classical plane geometry, however, lines are potentially infinite. What exists is only what we have actually drawn.
We do not, for example, imagine that a number -- number 1 -- is cut off from a pre-existing infinitude of numbers. (Don't we begin with number 1?) Nor do we think that an area, such as a square, is an "area segment" of some infinite plane. This quarrel about actual versus potential infinities arises only when a line is abstracted from the boundary of a figure. For we can speak of the "side" of a square -- as if there were a side apart from the square! The words are distinct, but they do not refer to any distinction in actuality. Analytic geometry, and modernism in general, gets distracted by these verbal and then logical distinctions. Plane geometry, on the other hand, is the study of figures; because a figure -- a whole form -- is what we actually see. Our idea of a figure -- a square, a pentagon -- comes first, and then we logically describe its physical construction. Is not plane geometry, then, the better point of view? For it is concerned with what we actually perceive, namely, figures.
Moreover, if we imagine something to be actually infinite, then it is never complete, never whole. Is it meaningful to say that something that is never whole exists?
A ray is a straight line with one extremity.
![]()
Next Lesson: The Pythagorean distance formula
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
