39
VARIATION
The constant of proportionality
THE SUBJECT OF VARIATION is more properly the subject of arithmetic, because it depends squarely on the concept of ratio. See Skill in Arithmetic, Lesson 16.
Direct variation
We say that a quantity a varies directly as a quantity b, if, when b changes, a changes in the same ratio.
This means that if b doubles in value, a will also double in value. If b increases by a factor of 3, then a will also increase by a factor of 3. While if the value of b becomes half, so will the value of a.
Let the initial values of a and b be a1, b1, and let their final values be
a2, b2. Then, a varies directly as b means: Proportionally,
a2 : a1 = b2 : b1
| " | The final value of a is the to initial value of a |
| as the final value of b is to the initial value of b." | |
Example 1. When b = 2, a = 7. What is the value of a when b = 10?
Solution. The value of b has gone from 2 to 10. That is, it has increased five times. Therefore, the value of a will increase five times. It will go from 7 to 35.
Formally,
a2 : a1 = b2 : b1.
a2 : 7 = 10 : 2.
10 is five times 2. Therefore, a2 will be five times 7.
Example 2. When b = 8, a = 4. What is the value of a when b = 13?
Solution. Proportionally,
a2 : a1 = b2 : b1.
That is,
a2 : 4 = 13 : 8.
Alternately, 4 is half of 8. Therefore, a2 will be half of 13, which is 6.5.
Problem 1. a varies directly as b. When b = 12, a = 27. What is the value of a when b = 4?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The value of b has gone from 12 to 4. Its final value, then, is a third of its initial value. Therefore, the final value of a will be a third of 27, which is 9.
Problem 2. When b = 6, a = 42. What is the value of a when b = 9?
a2 : a1 = b2 : b1.
a2 : 42 = 9 : 6.
Alternately, 42 is seven times 6. Therefore, a2 will be seven times 9, which is 63.
Or, 9 is one and a half times 6. (6 + 3 = 9.) Therefore, a2 will be one and a half times 42. 42 + 21 = 63.
The constant of proportionality
When a varies directly as b, we often say, "a is proportional to b." In that case, the relationship between a and b takes this algebraic form:
a = kb.
k is called the constant of proportionality. In actual scientific problems, it is determined by experiment. For example, in what is called Hooke's Law, the force F that a stretched spring exerts is proportional to the distance x that the spring has stretched.
F = kx.
In other words, the greater the stretch, the greater the force.
Example 3.
a) For a given spring, F has the value 35 when the spring has stretched 8
a) inches. What is the constant of proportionality for that spring?
Solution. F = kx. That is,
35 = k· 8
Therefore,
| k | = | 35 8 |
= 4 | 3 8 |
= 4.375 |
b) What is the value of F when the spring has stretched 11 inches?
Solution. For that spring, we have determined that
F = 4.375 x.
Therefore, when x = 11,
| F | = | 4.375 × 11 |
| = | 43.75 + 4.375 (Skill in Arithmetic, Lesson 8) | |
| = | 48.125 | |
In general, if a is proportional to b, and a1, b1 are observed values, then
a1 = kb1.
This implies:
![]()
Therefore,
![]()
When a varies directly as b, the constant of proportionality is the quotient of any observed or given values.
Note: The units on the right must equal those of a on the left -- distance, time, force, whatever they might be. a1, then, is the numerator and b1 the denominator: The units of b then cancel.
See the following problem.
Problem 3.
a) The distance d that an automobile travels varies directly as the time t
a) that it travels. After 2 hours, the car has traveled 115 miles. Write
a) the equation that relates d and t.
| d | = |
115 2 |
t | = | 57.5t |
b) The units on the right must be same as those of d on the left, that is,
a) distance. What are the units, then, of 57.5?
|
distance time |
The units of time then cancel, leaving only distance on both sides.
In this example, the constant of proportionality is the constant speed of the car: 57.5 miles per hour.
c) How far has the car traveled after 7 hours?
d = 57.5 × 7 = 402.5 miles.
As for Problems 1 and 2 above, while we could have solved them by finding the constant of proportionality, anyone who has to would show a lack of understanding of direct variation.
Problem 4. Prove: Varies directly is a transitive relation. That is, if a varies directly as b, and b varies directly as c, then a varies directly as c.
If a = k1b, and b = k2c, then a = k1k2c.
Problem 5. If the side of a square doubles, how will the perimeter change?
The perimeter will also double, because the perimeter varies as the side. P = 4s. The constant of proportionality is 4.
Problem 6.
a) If the diameter of a circle doubles, how will the circumference change?

The circumference will also double, because the circumference varies as the diameter.
b) What number is the constant of proportionality?
π. C = πD.
That constant has been the subject of investigation for over 2500 years.
Problem 7. If the diameter of a circle changes from 6 cm to 9 cm, by how much will the circumference change?
In going from 6 cm to 9 cm, the diameter has increased one and a half times; that is the ratio of 9 to 6. Therefore, the circumference will also increase one and a half times.
Problem 8. The circumference C of a circle varies directly as the perimeter of the circumscribed square.

What number is the constant of proportionality?
| π 4 |
. For, the side of the square is equal to the diameter D. |
Therefore the perimeter of the square is equal to 4D.
| And | C 4D |
= | 1 4 |
· | C D |
= | 1 4 |
· π | = | π 4 |
. |
Varies as the square
A quantity a varies as the square of a quantity b, if, when b changes, a changes by the square of that ratio. Thus, if b changes by a factor of 4, then a will change by a factor of 4² = 16. If b changes to one third of its value, then a will change to one ninth of its value.
![]()
Problem 9. a varies as the square of b. When b = 7, a = 4. What is the value of a when b = 35?
In going from 7 to 35, b has changed by a factor of 5. a therefore will change by a factor of 5² = 25. a = 25· 4 = 100.
Problem 10. a varies as the square of b. When b = 20, a = 32. What is the value of a when b = 15?
In going from 20 to 15, b has become three fourths of its value. 15 is three fourths of 20. a therefore will become nine sixteenths of its value.
| 9 16 |
× 32 = 18 |
Theorem. If a varies directly as b, then a² will vary as b².
This is easily proved if we write the ratios in fractional form.
a varies directly as b means:
![]()
Therefore, on squaring both sides:
![]()
This implies
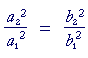
This means that a² varies as b²; which is what we wanted to prove.
Problem 11. The area A of a circle varies directly as the area of the circumscribed square. That is, as the area of the square changes, the area

of the circle changes proportionally.
a) Show that this implies that the area A of the circle varies as the
a) square of the radius r.
The side of the circumscribed square is equal to the diameter D of the circle. Therefore the area of the circumscribed square is equal to D². Hence the area A of the circle varies as D².
But D varies directly as r -- D = 2r -- and therefore, according to the theorem, D² varies as r². Therefore, since A varies as D², and D² varies as r², then transitively, A varies as r². The area of the circle varies as the square of the radius.
b) If the radius of a circle changes from 6 cm to 12 cm, how will the
b) area change?
In going from 6 cm to 12 cm, the radius has doubled, that is, it has changed by a factor of 2. The area therefore will change by a factor of 2² = 4. It will be four times larger.
c) What is the constant of proportionality that relates the area A to r²?
π. A = πr².
Example 4. The surface area of a sphere.
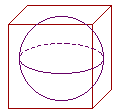
The surface area of a sphere is proportional to the surface area of the circumscribed cube.
Now, each face of the cube is a square whose side is equal to the diameter D of the sphere. And a cube has 6 faces. Therefore, the surface area of the cube is equal to 6D².
In other words, the surface area A of a sphere is proportional to the square of its diameter.
Do you know what the constant of proportionality is?
π. A = πD²
Problem 12. Show that the surface area of a sphere varies as the square of its radius. Write the equation that relates the surface area A to the radius r.
Since A = πD², and D = 2r, then A = π(2r)² = 4πr².
Section 2: Varies inversely. Varies as the inverse square.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
