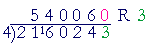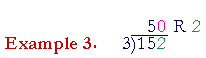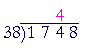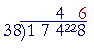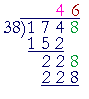S k i l l
i n
A R I T H M E T I C

Lesson 11

SHORT DIVISION

Division means finding what number times the divisor will equal the dividend. (Lesson 10.) To help us find that number, there is a technique called short division.

In this Lesson, we will answer the following:

When we write the division box, where do we write the divisor?
How do we do short division?
When the dividend is a decimal, where does the point go in the quotient?
Section 2
How do we round off, or approximate, a decimal to a given number of decimal places?
How do we express the quotient as a decimal?

Dividend ÷ Divisor = Quotient

Example. Using the division box, write 1 ÷ 4. (There is nothing to calculate.)

Answer. 4 is the divisor. It goes outside the box.

Before going on to short division, the student should be clear about division with remainder.

2.	How do we do short division?

	From the left of the dividend (252), take as many digits as necessary to form a number (25) that will contain the divisor (7) at least once but less than ten times. Divide that partial dividend by the divisor, and obtain the first digit of the quotient (3). Write that digit over the last digit of the partial dividend (5) -- and write the remainder (4) beside the next digit of the dividend. Continue the operation.

"7 goes into 25 three (3) times (21) with 4 left over."

Write the remainder 4 beside the 2. Continue:

"7 goes into 42 six (6) times exactly."

Begin, "5 goes into 17 three (3) times (15) with 2 left over."

Write 3 over the 7 (not over the 1), and write the remainder 2 next to the 9.

Continue: "5 goes into 29 five (5) times (25) with 4 left over.

Write 5 over the 9, and write the remainder 4 next to the 8.

Finally, "5 goes into 48 nine (9) times (45) with 3 left over."

Write 9 over the 8. The final remainder is 3.

This problem will illustrate the following point:

Over every digit in the dividend
we must write a digit in the quotient.
We proceed one digit at a time.

We will write a digit over the 1, then over the 6, then over the 0, and so on, until finally we write a digit over the 3.

Begin,

"4 goes into 21 five (5) times (20) with remainder 1 ."

Next, "4 goes into 16 four (4) times exactly."

Next, "4 goes into 0 zero (0)."

Whenever the partial dividend is less than the divisor
-- 0 is less than 4 -- write 0 in the quotient.

Next, we must write a digit over the 2: "4 goes into 2 zero (0)."

Now the 2 remains. It is the remainder.

Whenever the quotient is 0, that digit beneath it
in the dividend is the remainder.

"4 goes into 24 six (6) times exactly."

Finally, "4 goes into 3 zero (0)."

3 is the final remainder.

Again, whenever the quotient is 0, the digit beneath it in the dividend remains.

"3 goes into 15 five (5) times. 3 goes into 2 zero (0)."

2 is the remainder.

That is, 152 = 50 × 3 + 2.

We use short division whenever it is easy to multiply the divisor.

Example 4. Harold has a debt of $3,164. He is able to pay $25 a week. How many weeks will it take him to pay the debt?

Solution. How many 25's will equal 3,164. To find out, we must divide:

"25 goes into 31 one (1) time (25) with 6 left over."

"25 goes into 66 two (2) times (50) with 16 left over."

"25 goes into 164 six (6) times (150) with 14 left over."

At the end of 126 weeks, then, the debt will be almost paid. $14 will remain. Therefore, it will take Harold 127 weeks.

We have seen that the divisor must be a whole number. We can now consider the case in which the dividend is a decimal.

3.	When the dividend is a decimal, and the divisor a whole number, how do we proceed?

	Divide in the usual way. But on coming to the decimal point, place a decimal point above it in the quotient, and continue the operation.

"9 goes into 27 three (3) times."

"9 goes into 3 zero (0)."

Place the point in the quotient. The 3 remains.

"9 goes into 36 four (4) times.

Solution. The divisor 7 is a whole number. Place the point:

When we have placed the point has been placed, then over each digit in the dividend we must write a digit in the quotient.

For those students still required to do problems in which the divisor has two or more digits, we include the following example. Note, however, that it can be done with short division.

Example 7.

38 will not go into 1; and it will not go into 17; but it will go into 174. The question is, How many times? To answer,

Try the first digit of the divisor, 3, into the first two digits of the dividend, 17.

3 goes into 17 five times. Therefore we do not have to try any number greater than 5. (Because any number greater than 5 × 38 will be too big. 5 × 30 = 150, which is less than 174, but 6 × 30 = 180; too big.)

5, in fact, is too big: 5 × 38 = 150 + 40 = 190.

(The student should try to do these simple multiplications mentally. It is the most efficient way to test a digit for the quotient.)

3 will go into 174 four (4) times: