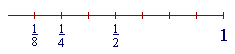S k i l l
i n
A R I T H M E T I C

Lesson 23

FRACTIONS
INTO DECIMALS

In this Lesson, we will answer the following:

What is a "decimal"?
If the denominator is not a power of 10, how can we change the fraction to a decimal?
Frequent decimals and percents: Half, quarters, eighths, fifths.
Section 2
What is a general method for expressing a fraction as decimal? Complete versus incomplete decimals.

1.	What is a "decimal"?

	A "decimal" is a fraction whose denominator we do not write but which we understand to be a power of 10. The number of decimal places indicates the number of zeros in the denominator.

The number of decimal places is the number of digits to the right
of the decimal point. (Lesson 3, Question 4.)

Example 1.

.8	=	8 10	One decimal place; one 0 in the denominator.
.08	=	8 100	Two decimal places; two 0's in the denominator.
.008	=	8 1000	Three decimal places; three 0's in the denominator.
And so on.

The number of decimal places indicates the power of 10.

Example 2. Write as a decimal:

614
100,000

Answer.

614
100,000

= .00614

Five 0's in the denominator indicate five digits after the decimal point.

The five 0's in the denominator is not the number of 0's in the decimal!

Alternatively, in Lesson 10 we introduced the division bar, and in Lesson 3 we saw how to divide a whole number by a power of 10.

614
100,000

614 ÷ 100,000 = .00614

Separate five decimal places.

Example 3. Write this mixed number as a decimal: 6

49
100

Answer. 6

49
100

= 6.49

The whole number 6 does not change. We simply replace the

common fraction

49
100

with the decimal .49.

Example 4. Write this mixed number with a common fraction: 9.0012

Answer. 9.0012 = 9

12
10,000

Again, the whole number does not change. We replace the decimal

.0012 with the common fraction

12
10,000

. The decimal .0012 has four

decimal places. The denominator 10,000 is a 1 followed by four 0's.

This accounts for fractions whose denominator is already a power of 10.

2.	If the denominator is not a power of 10, how can we change the fraction to a decimal?

	Make the denominator a power of 10 by multiplying it or dividing it.

Example 5. Write

9
25

as a decimal.

Solution. 25 is not a power of 10, but we can easily make it a power of 10 -- 100 -- by multiplying it by 4. We must also, then, multiply the numerator by 4.

4
5

4
5

We can make 5 into 10 by multiplying it -- and 4 -- by 2.

Example 7. Write as a decimal:

We can make 200 into 1000 by multiplying it -- and 7 -- by 5.

Alternatively, according to the properties of division,

7 200	=	_ 7 _ 2 × 100	=	3.5 100	, on dividing 7 by 2,

			=	.035,	on dividing 3.5 by 100.

Example 8. Write as a decimal:

Here, we can change 200 into a power of 10 by dividing it by 2. We can do this because 8 also is divisible by 2.

Or, again,

Example 9. Write as a decimal:

We can change 400 to 100 by dividing it -- and 12 -- by 4.

To summarize: We go from a larger number to a smaller by dividing (Examples 8 and 9); from a smaller number to a larger by multiplying (Example 5).

Frequent decimals

The following fractions come up frequently. The student should know their decimal equivalents.

1
2

1
4

3
4

1
8

3
8

5
8

7
8

1
3

2
3

1
2

1
4

1
4

1
2

Therefore, its decimal will be half of .50 --

1
4

3
4

1
4

3 4	= 3 × .25 = .75

Next,

1
8

. But

1
8

is half of

1
4

Therefore, its decimal will be half of .25 or .250 --

1
8

= .125

The decimals for the rest of the eighths will be multiples of .125.

Since 3 × 125 = 375,

3 8	= 3 × .125 = .375

Similarly,

5
8

will be 5 ×

1
8

= 5 × .125.

5 × 125 = 5 × 100 + 5 × 25 = 500 + 125 = 625.

(Lesson 8) Therefore,

5
8

= .625

Finally,

7
8

= 7 × .125.

7 × 125 = 7 × 100 + 7 × 25 = 700 + 175 = 875.

Therefore,

7
8

= .875

These decimals come up frequently. The student should know how to generate them quickly.

The student should also know the decimals for the fifths:

1
5

2
10

= .2

The rest will be the multiples of .2 --

2 5	=	2 ×	1 5	= 2 × .2 = .4

3 5	= 3 × .2 = .6

4 5	= 4 × .2 = .8

Example 10. Write as a decimal: 8

3
4

Answer. 8

3
4

= 8.75

The whole number does not change. Simply replace the common

fraction

3
4

with the decimal .75.

Example 11. Write as a decimal:

7
2

Answer. First change an improper fraction to a mixed number:

7
2

= 3

1
2

= 3.5

"2 goes into 7 three (3) times (6) with 1 left over."

Then repalce

1
2

with .5.

Example 12. How many times is .25 contained in 3?

Answer. .25 =

1
4

. And

1
4

is contained in 1 four times. (Lesson 19.)

Therefore,

1
4

, or .25, will be contained in 3 three times as many times. It will

be contained 3 × 4 = 12 times.

Example 13. How many times is .125 contained in 5?

Answer. .125 =

1
8

. And

1
8

is contained in 1 eight times. Therefore,

1
8

or .125, will be contained in 5 five times as many times. It will be contained 5 × 8 = 40 times.

As for

1
3

and

2
3

, they cannot be expressed exactly as a decimal.

However,

1
3

.333

And

2
3

.667

See Section 2, Question 3.

Frequent percents

From the decimal equivalent of a fraction, we can easily derive the percent: Move the decimal point two places right (Lesson 3.) Again, the student should know these. They come up frequently.

1 2	=	.50	=	50%

1 4	=	.25	=	25%

3 4	=	.75	=	75%

1 8	=	.125	=	12.5% (Half of	1 4	.)

3 8	=	.375	=	37.5%

5 8	=	.625	=	62.5%

7 8	=	.875	=	87.5%

1 5	=	.2	=	20%

2 5	=	.4	=	40%

3 5	=	.6	=	60%

4 5	=	.8	=	80%

In addition, the student should know

1 3	= 33	1 3	%

2 3	= 66	2 3	%

(Lesson 15)

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: themathpage@nyc.rr.com

FRACTIONS INTO DECIMALS

FRACTIONS
INTO DECIMALS