|
Lesson 25 MULTIPLYING FRACTIONS
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 × | 2 7 |
("3 times | 2 7 |
"). What does that mean? |
According to the meaning of multiplication,
| 3 × | 2 7 |
= | 2 7 |
+ | 2 7 |
+ | 2 7 |
That is,
| 3 × | 2 7 |
= | 2 + 2 + 2 7 |
= | 6 7 |
. | |
We can therefore state the "rule" as follows:
| 1. | How do we multiply a fraction by a whole number? |
|
|
|
| Multiply the numerator by the whole number. | |
| Example 1. | 2 × | 4 9 |
= | 8 9 |
| Example 2. | 6 × | 2 5 |
= | 12 5 |
= 2 | 2 5 |
Example 3. Multiplying a mixed number.
| 2 × 4 | 1 3 |
= 8 | 2 3 |
Distribute the multiplier 2 -- first to the whole number, then to the
| fraction. (For, 4 | 1 3 |
means 4 + | 1 3 |
.) |
| 2 × 4 = 8. And | 2 × | 1 3 |
= | 2 3 |
. |
When multiplying by a whole number, it is not necessary to change to an improper fraction.
This is exactly what we did to multiply dollars and cents (Lesson 8).
4 × $6.20 = $24 + $.80 = $24 .80
| Example 4. | 5 × 3 | 2 11 |
= 15 | 10 11 |
Now, if the fraction becomes improper, change it to a mixed number. (Lesson 19, Question 8 .)
| Example 5. | 7 × 6 | 3 5 |
= 42 | 21 5 |
= 42 + 4 | 1 5 |
= 46 | 1 5 |
Example 6. Dividing first.
| 15 × | 2 3 |
= | 5 × 2 | = | 10. |
"3 goes into 15 five (5) times. 5 times 2 is 10."
The order of multiplying and dividing does not matter, and so we may always divide first. This results in multiplying smaller numbers.
(See Some properties of division, Property 3.)
| Example 7. | 20 × | 11 5 |
= | 4 × 11 | = | 44. |
"5 goes into 20 four (4) times."
| 2. | How do we multiply a fraction by a fraction? |
|
|
|
| Multiply the numerators and multiply the denominators. | |
For the meaning of multiplying by a fraction, see the next Lesson.
| Example 8. | 3 4 |
× | 7 11 |
= | 21 44 |
When multiplying fractions, do not change to a common denominator.
| Example 9. | 8 9 |
× | 15 16 |
If any numerator has a divisor in common with any denominator, then we can cancel.
8 and 16 have a common divisor, which is 8 itself. 9 and 15 have a common divisor, 3.

"8 goes into 8 once (1); 8 goes into 16 two (2) times."
"3 goes into 9 three (3) times; 3 goes into 15 five (5) times."
"1 × 5 = 5. 3 × 2 = 6."
| Example 10. | 1 2 |
× | 3 4 |
× | 5 7 |
= | 15 56 |
Multiply all the numerators: 1 × 3 × 5 = 15
Multiply all the denominators: 2 × 4 × 7 = 8 × 7 = 56
The time to cancel is before multiplying when the numbers are smaller. If nothing cancels before , as in this example, then the answer is already in its lowest terms.
| Example 11. | 4 3 |
× | 9 2 |
2 is a common divisor of 4 and 2. 3 is a common divisor of 3 and 9.

"2 goes into 4 two (2) times; 2 goes into 2 one (1) time."
"3 goes into 3 one (1) time; 3 goes into 9 three (3) times."
"2 × 3 = 6. 1 × 1 = 1."
| A fraction with denominator 1 ( | 6 1 |
) is simply the numerator. It is not |
necessary to say "1 goes into 6 six times."
Here is another example:
| 5 1 |
= 5 |
| Example 12. | 4 × | 5 6 |
We may cancel before multiplying 4 × 5:
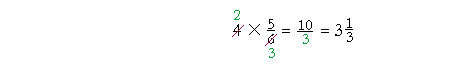
"2 goes into 4 two (2) times."
"2 goes into 6 three (3) times."
"2 × 5 = 10; over 3."
We would cancel after multiplying 4 × 5; and so we may cancel before. Again, the advantage of canceling first is that we work with smaller numbers.
| 3. | How do we multiply a mixed number by a mixed number, or a fraction by a mixed number? |
| Change the mixed numbers to improper fractions. | |
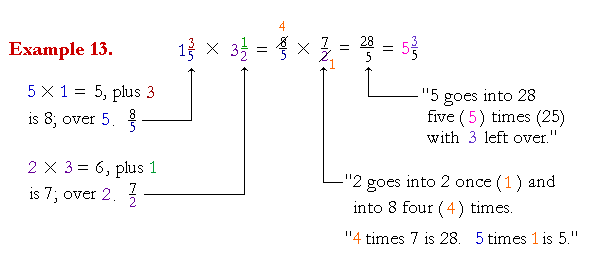
This is the only place in arithmetic where it is necessary to change to an improper fraction.
| Example 14. | 2 × 4 | 1 3 |
= 8 | 2 3 |
It is not necessary to change to an improper fraction. When multiplying by a whole number, multiply the whole number times the whole number, and multiply the whole number times the numerator.
The following is a ratio and proportion problem. It depends on understanding mixed ratio, Lesson 17.
Example 15. If 6 workers can paint 8 rooms in 10 hours, how long will it take 15 workers to paint 14 rooms?
Solution. How many rooms can 6 workers paint in ONE hour?
Since they can paint 8 rooms in 10 hours, then in 1 hour they can paint
| 8 10 |
= | 4 5 |
of a room. |
(That is the number of rooms per hour. Lesson 10.)
Now, what ratio has 15 workers to 6?
| 15 6 |
= 2 | 3 6 |
= 2½. |
There are 2½ times as many workers. Therefore in 1 hour, they will be able to paint 2½ times as many rooms.
| 2½ × | 4 5 |
= | 5 2 |
× | 4 5 |
= 2. |
In 1 hour, then, 15 workers can paint 2 rooms. Therefore to paint 7 × 2 rooms will require 7 hours.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2: Dividing fractions
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
