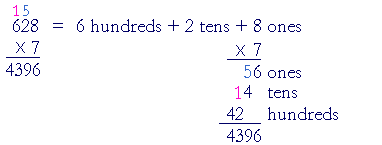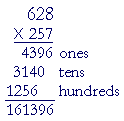|
Lesson 9 MULTIPLY WHOLE NUMBERS
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
"7 times 8 is 56." Write 6, carry 5. "7 times 2 is 14, plus 5 is 19." Write 9, carry 1. "7 times 6 is 42, plus 1 is 43." Write 43. We can analyze this as follows:
7 has been distributed to each unit of 628: to 6 hundreds + 2 tens + 8 ones. On the left (but compare the right): 7 × 8 ones = 56 ones, or simply 56. Write 6 below the line and carry the 5 onto the tens column, because the 5 is 5 tens. Next: 7 × 2 tens = 14 tens, plus 5 are 19 tens. Write 9 and carry the 1 onto the hundreds column -- because 19 tens = 190. The carried 1 is 1 hundred. Finally: 7 × 6 hundreds = 42 hundreds, plus 1 is 43 hundreds. Write 43. When the multiplier has more than one digit --
-- follow the same procedure for each digit. However, when we multiply by 5 tens, the product is 3140 tens. Therefore we write 0 in the tens column. When we multiply by 2 hundreds, the product is 1256 hundreds, and so we write 6 in the hundreds column. We can state the rule as follows: |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
Anticipating the next Question, if there were decimal points --
-- the multiplication would proceed in exactly the same way. In the answer, we would then separate as many decimal places as there are in the two numbers together; in this case, three.
On multiplying by 7 ones, write 2 in the ones column. On multiplying by 3 tens, write 8 in the tens column -- because the partial product 288 means 288 tens. Rather than do the traditional method of "carrying," the student should be able to calculate each partial product mentally by distributing from left to right. We have indicated this above. Example 2. 0's within the multiplier.
On distributing 8 ones, write 6 in the ones column. Any number times 0 is 0, therefore it is not necessary to write any digit in the tens column. On distributing 3 hundreds, write 1 in the hundreds column. It is not necessary to write rows of 0's. They add nothing to the product. |
|||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
|
Example 3. .2 × 6.03 Solution. Ignore the decimal points. Simply multiply 2 × 603 = 1206 Now we must put back the decimal points. Together, .2 and 6.03 have three decimal places. (Lesson 3, Question 4.) Therefore, starting from the right, separate three places: 1.206 When we ignore a decimal point, we have in effect moved the point to the right: 6.03 → 603 We have multiplied by a power of 10. (Lesson 3, Question 2.) Therefore, to compensate and name the right answer, we must divide by that power, we must separate the same number of decimal places. Example 4. .03 × .002 Solution. Ignore the decimal points. 3 × 2 = 6 Together, .03 and .002 have five decimal places. Therefore, separate five places: .00006 Example 5. 200 × .012 Solution. Ignore the decimal point. Multiply 200 × 12 = 2400 Again, to multiply whole numbers that end in 0's, first ignore the 0's, then replace them. (Lesson 8, Question 2.) But replace only the 0's on the end of whole numbers. Do not replace the 0 of .012 Now separate three decimal places (.012): 2.400 = 2.4 How can we find a percent of a number? We have seen (Lesson 3) that finding a percent of a number involves multiplication. 8% of $400 = 8 × $4 = $32. How much, then, is 6% of $75? Again, we can analyze as follows: 1% of $75 is $.75. Therefore, 6% of $75 = 6 × $.75. 6 × 75 = 420 + 30 = 450 On separating two decimal places (.75): 6% of $75 = $4.50 Example 6. How much is 9% of $84? Solution. Simply multiply 9 × 84, then separate two places. 9 × 84 = 720 + 36 = 756 Therefore, 9% of $84 = $7.56. Example 7. How much is 3% of $247? Solution. 3 × 247 = 600 + 120 + 21 = 741. Therefore, 3% of $247 = $7.41 Example 8. How much is 11% of $76? Solution. 11 × 76 = 760 + 76 = 836 Therefore, 11% of $76 = $8.36. These are simple problems that do not require a calculator. For more such simple problems, see Lesson 28. To learn how to do percent problems with a calculator, see Lesson 13. Area of a rectangle What is "1 square foot"?
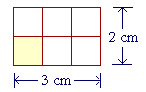
1 square foot is a square figure in which each side is 1 foot. We abbreviate "1 square foot" as 1 ft². Now here is a rectangle whose base is 3 cm and whose height is 2 cm.
What do we call the small shaded square? Since each side is 1 cm, we call it "1 square centimeter." And we can see that the entire figure is made up 2 × 3 or 6 of them! In other words, the area of that rectangle -- the space enclosed by the boundary -- is 6 square centimeters: 6 cm².
If the rectangle were 3 by 3 -- that is, if it were a square -- then it would be made up of 9 cm². If it were 3 by 4, the area would be 12 cm². And so on. In every case, to calculate the area of a rectangle, we multiply the base times the height. Area = Base × Height When the length is measured in centimeters, the area is measured in square centimeters: cm². And similarly for any unit of length. We have illustrated this with whole numbers, but it will be true for any numbers.
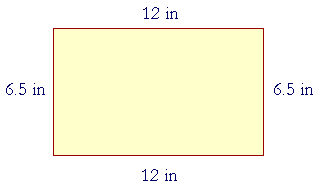
If the base is 12 in, and the height is 6.5 in, then to find the area, multiply 12 × 6.5. Now, 12 × 65 = 650 + 130 = 780 Therefore on separating one decimal place (6.5): Area = 78 in² Please "turn" the page and do some Problems. or Continue on to the Next Lesson. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
|||||||||||||||||||||||||||||||||||