2
RATIONAL AND IRRATIONAL NUMBERS
Which numbers have rational square roots?
The decimal representation of irrationals
LET US BEGIN by recalling that a variable is a symbol that takes on values. A value is a number.
Thus, if x is a variable, then x might have the value 2, or −3, or 5.2, and so on.
Next, the following are called the integers:
0, ±1, ±2, ±3, and so on.
± ("plus or minus") is called the double sign.
And the following are called the square numbers, or the perfect squares:
1 4 9 16 25 49 64 . . .
For, these are the numbers 1· 1, 2· 2, 3· 3, 4· 4, and so on.
Rational and irrational numbers
1. What are the rational numbers?
They are the numbers of arithmetic: The whole numbers, fractions, mixed numbers, and decimals; together with their negative images.
2. Which of the following numbers are rational?
| 1 | −6 | 3½ | − | 2 3 |
0 | 5.8 | 3.1415926535897932384626433 |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
All of them! All decimals are rational. That long one is an approximation to π.
3. A rational number can always be written in what form?
| As a fraction | a b |
, where a and b are integers (b |
When a and b are positive, that is, when they are natural numbers, then we can always name their ratio. Hence the term, rational number.
At this point, the student might wonder, What is a number that is not rational?
An example of such a number is ![]() ("Square root of 2").
("Square root of 2"). ![]() is not a number of arithmetic: there is no whole number, no fraction, and no decimal whose square is 2. (1.414 is close, because (1.414)² = 1.999396 -- which is almost 2.)
is not a number of arithmetic: there is no whole number, no fraction, and no decimal whose square is 2. (1.414 is close, because (1.414)² = 1.999396 -- which is almost 2.)
To prove that there is no rational number whose square is 2, suppose
| there were. Then we could express it as a fraction | m n |
in lowest terms. |
That is, suppose
| m n |
· | m n |
= | m· m n· n |
= 2. |
| But that is impossible. Since | m n |
is in lowest terms, then m and n have |
no common divisors except 1. Therefore, m· m and n· n also have no common divisors -- they are relatively prime -- and it will be impossible to divide n· n into m· m and get 2![]()
There is no rational number whose square is 2. Therefore we call ![]() an irrational number.
an irrational number.
By recalling the Pythagorean theorem, we can see that these irrational
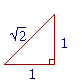 numbers are necessary. For if the sides of an isosceles right triangle are called 1, then we will have 1² + 1² = 2, so that the hypotenuse is
numbers are necessary. For if the sides of an isosceles right triangle are called 1, then we will have 1² + 1² = 2, so that the hypotenuse is ![]() . There really is a length that logically deserves the name, "
. There really is a length that logically deserves the name, "![]() ." Inasmuch as numbers name the lengths of lines, then
." Inasmuch as numbers name the lengths of lines, then ![]() is a number.
is a number.
4. Which numbers have rational square roots?
Only the square roots of the square numbers.
![]() = 1 Rational
= 1 Rational
![]() Irrational
Irrational
![]() Irrational
Irrational
![]() = 2 Rational
= 2 Rational
![]() ,
, ![]() ,
, ![]() ,
, ![]() Irrational
Irrational
![]() = 3 Rational
= 3 Rational
And so on.
Only the square roots of square numbers are rational.
The existence of these irrationals was first realized by Pythagoras in the 6th century B.C. He called them "unnameable" or "speechless" 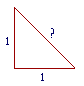 numbers. For if we ask, "In the isosceles right triangle, what ratio has the hypotenuse to the side?" -- we cannot say. We can name it only as "Square root of 2."
numbers. For if we ask, "In the isosceles right triangle, what ratio has the hypotenuse to the side?" -- we cannot say. We can name it only as "Square root of 2."
5. Say the name of each number.
a) ![]() "Square root of 3."
b)
"Square root of 3."
b) ![]() "Square root of 5."
"Square root of 5."
c) ![]() "2." This is a rational -- nameable -- number.
"2." This is a rational -- nameable -- number.
d) ![]() "Square root of 3/5."
e)
"Square root of 3/5."
e) ![]() "2/3."
"2/3."
The decimal representation of irrationals
When we express a rational number as a decimal, then either the decimal will terminate -- we say it will be complete -- or there will be a predictable pattern of digits. But if we attempted to express an irrational number as a complete decimal, then, clearly, we could not, because if we could, the number would be rational![]()
Moreover, there will not be a predictable pattern of digits. For example,
![]()
![]() 1.4142135623730950488016887242097
1.4142135623730950488016887242097
Now, with rational numbers you sometimes see
| 1 11 |
= | .090909. . . |
| The three dots (ellipsis) mean, "It is not possible to express | 1 11 |
exactly as a decimal. However we can approximate it to as many decimal places as we please according to the indicated pattern; and the more
| decimal places we take, the closer we will come to | 1 11 |
." |
| We say that any decimal for | 1 11 |
is incomplete. But the decimal for ¼, |
for example, which is .25, is complete.
The decimal for any irrational number, however, is always incomplete. An example is the decimal for ![]() above.
above.
If we write ellipsis --
![]() = 1.41421356237. . .
= 1.41421356237. . .
-- we mean, "It is not possible to express ![]() exactly as a decimal. The decimal you see is a rational approximation. We could continue the approximation for as many decimal places as we please according to the rule or method for calculating the next digit (not the subject of these Topics), and again, the more decimal places we calculate, the closer we will come to
exactly as a decimal. The decimal you see is a rational approximation. We could continue the approximation for as many decimal places as we please according to the rule or method for calculating the next digit (not the subject of these Topics), and again, the more decimal places we calculate, the closer we will come to ![]() ."
."
It is important to understand that no one has ever beheld the value of any irrational number. (π? What is its value? 3.14159? Not quite.) Our knowledge of an irrational number is only as a rational approximation. And if we choose a decimal approximation, then the more decimal places we calculate, the closer we will be to the value.
One sometimes hears that a real number, such as ![]() , "is"
, "is"
an infinite decimal:
![]() = 1.41421356237. . .
= 1.41421356237. . .
But anything we imagine to be infinite is never complete, never whole. And can something that is never whole ever be equal to anything?
In calculus, the student will see that an irrational number exists only as the limit of the sequence of its rational approximations.
Real numbers
5. What is a real number?
Any number that you would expect to find on the number line. It is a number required to label any point on the number line. It is a number whose absolute value names the distance of any point from 0.
6. What are the two main categories of real numbers?
Rational and irrational.
Problem. We have categorized numbers as real, rational, irrational, and integer. Name all the categories to which each of the following belongs.
| 3 Real, rational, integer. | −3 Real, rational, integer. | |
| −½ Real, rational. | |
|
| 5¾ Real, rational. | − 11/2 Real, rational. | |
| 1.732 Real, rational. | 6.920920920. . . Real, rational. | |
| 6.9205729744. . . Real. And let us assume that it is irrational, that is, that the digits do not repeat. Moreover, we must assume that there is a rule for computing each next digit. For if there were not, then we would have no idea which irrational number this is! | ||
| 6.9205729744 Real, rational. Any complete decimal is rational. | ||
7. What is a real variable?
A variable whose values are real numbers.
Calculus is the study of functions of a real variable.
Problem. Let x be a real variable, and let 3 < x < 4. Name five values that x might have.
![]()
*
To learn about the evolution of the real numbers starting with the natural numbers, click here.
www.proyectosalonhogar.com
