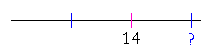S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

PERCENT OF A NUMBER

Lesson 28  Section 2


To find the Base

We have seen (Lesson 27) that finding the Amount involves multiplication.  To find

3% of $600,

where $600 is the Base, first name 1%:

1% of $600 is $6.00.

Therefore, 3% is

3 × $6.00 = $18.00.

But say that we are given $18.00, and we ask:

$18.00 is 3% of how much?

In other words,

3 × ? = $18.00?

To find the Base, then, we have to divide.

$18 ÷ 3 = $6.

But $6 is 1% of the Base.  The Base itself is 100 times that.

$18 is 3% of $600.

And we could check that.  1% of $600 is $6.00.  So 3% is 3 × $6.00 = $18.00.
 3.   How can we find the Base when we know the Amount and the Percent?
 
$18 is 3% of _?_
 
  Base = Amount ÷ Percent × 100

Example 1.   $36 is 4% of how much?

Answer.  The Base -- the number that follows "of" -- is missing.  And

$36 ÷ 4 = $9

But $9 is 1% of the Base.  The Base itself is 100 times that.

$36 is 4% of $900.

Let's check that.  1% of $900 is $9.  Therefore, 4% is 4 × $9 = $36.

 Formally, if we wrote 4% as    4 
100		 , then
36 ÷ 4% = 36 ÷   4 
100		  = 36 × 100
  4		  = 36 ÷ 4 × 100.

Example 2.   42 is 6% of what number?  Check the answer.

Answer.  42 ÷ 6 = 7; times 100 = 700.

Here is the check:

1% of 700 = 7.  Therefore, 6% = 6 × 7 = 42.  

Example 3.   8% of what number is 20?

   Answer.   20 ÷ 8 = 2 4
8		  = 2 1
2		 ; times 100 = 250.

20 is 8% of 250.

Check:

1% of 250 = 2.5

Therefore, 8% = 8 × 2.5 =  =  2.5 × 8 (Two and a half times 8)
 
   =  20.
  Example 4.   14 is 66 2
3		 % of what number?

Answer.  The problem asks:

14 is two thirds of what number?

But if 14 is two thirds, then half of 14 is one third.  Half of 14 is 7.  And 7 is one third -- of 21.

14 is 66 2
3		 % of 21.

Example 5.   30 is 60% -- three fifths -- of what number?

Answer.  If 30 is three fifths of some number,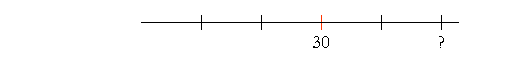

then a third of 30 is one fifth.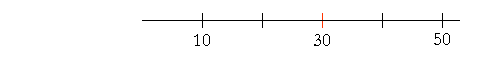  

A third of 30 is 10.  And 10 is one fifth -- of 50.

Example 6.   24 is 150% of what number?

  Answer.  150% is represented by the number 1½, or  3
2		 .  Let us resort to

the formal method (Lesson 25, Example 8):

24 is 150% of -- 1½ times -- 16.   (16 + 8 = 24.)

Thus, if the Amount is more than 100% of a number -- 24 is 150% of 16 -- then that number will be less than the Amount.  Therefore, multiply the Amount by the reciprocal of the fractional form of the percent.

Example 7.   36 is 225% of what number?

  Solution.   225% = 2¼ =  9
4		 .  Multiply 36 by  4
9		 .

Example 8.   Maria is retired and withdraws money from her retirement account.  But a tax of 20% is automatically withheld.  If she needs $1200, how much must she actually request?

Solution.   Since 20% will be withheld, Maria will receive 80% of her request.  So the question is:  $1200 is 80% of how much?

To calculate that, we must divide 1200 by .8 or, equivalently,  4
5		 .  But
  that will result in multiplying by  5
4		  or 1¼.  In other words, she must

request one and a quarter times, or one quarter more, than what she actually needs.

One quarter of $1200 is $300.  Therefore she must withdraw $1500.

It is then a simple matter to see that 20%, or one fifth, of $1500 is $300, so that her net amount will in fact be $1200.


Please "turn" the page and do some Problems.

or


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com