Trigonometry

The Topics | Home

11

THE CIRCLE


A CIRCLE IS A PLANE FIGURE bounded by one line, called the circumference, such that all straight lines drawn from the center to the circumference, are equal to one another.

A straight line from the center to the circumference is a called a radius.  A diameter is a straight line through the center and terminating in both directions on the circumference.

A radius, then, is half of a diameter; or, equivalently, a diameter is twice a radius:

D = 2r.


The definition of π

The student no doubt knows a value for the famous number π — 3.14 — but that is not its definition.  What, in fact, is the meaning of the symbol "π"?

π symbolizes the ratio -- the relationship with respect to relative size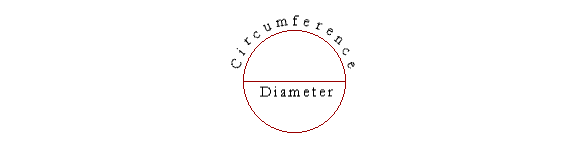
-- of the circumference of circle to its diameter, whatever that relationship might be.

So when we say that π = 3.14, we mean that the circumference of circle is a little more than three times longer than the diameter.

C
D		   =  π3.14

π turns out to be a fascinating yet difficult number, because it indicates the ratio of a curved line to a straight.  In the next Topic, we will see how π can be approximated.


Meanwhile, since

C
D		   =  π,

then we use that as a formula for calculating the circumference of a circle:

C = πD

Or, since D = 2r,

C = π· 2r = 2πr.

Problem 1.   Calculate the circumference of each circle.  Take π = 3.14.

To see the answer, pass your mouse over the colored area.  To cover the answer again, click "Refresh" ("Reload").

a)   The diameter is 5 cm.   3.14 × 5 = 15.7 cm

b)   The radius is 5 cm.   3.14 × 2 × 5 = 3.14 × 10 = 31.4 cm

Problem 2.    The average distance of the earth from the sun is approximately 93 million miles; assuming that the earth's path around the sun is a circle, approximately how many miles does the earth travel in a year?

C = π × 2r = 3.14 × 2 × 93 million = 584.04 million miles.

It is possible to prove that the area A of a circle is given by the formula,

A =  π
4		 D² = πr².

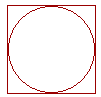
To gain some insight into that, let us circumscribe a square about the circle.

A circumscribed square

Now the side of the square is equal to the diameter D.  Therefore we know that the area of the square is D².  The question is,

What ratio has the circle to the circumscribed square?

A
D²		   =  ?

If we can answer that -- if we can express that ratio by some number k -- then the area of the circle will be

A = kD².

First, though, let us answer an easier question:

What ratio has the circumference of the circle
to the perimeter of the circumscribed square?

That is, what ratio has the boundary to the boundary?

A circumscribed square

Since the side of the square is equal to the diameter D, then the perimeter of the square is 4D.

And since, by definition,

C
D		   =  π,

then on dividing by 4,

 C 
4D		   =   π
4		  .  .  .  .  .  .  .  .  .  .  .  . (1)

A circumscribed square

π
4		  thus signifies the ratio of the circumference of a circle to the

perimeter of the circumscribed square.  And since π is a bit more than 3, we see that the circumference is a bit more than three fourths of that perimeter.

We are about to see that  π
4		  may be more fundamental than π itself.

For if we could prove that the area of a circle is

A =  π
4		 D²,
  so that   A
D²		   is also equal to  π
4		  --
A
D²		   =   π
4		 ,    compare line (1),

-- then we would have one of the most remarkable theorems in all of mathematics:

 C 
4D		   =   A
D²

A circumscribed square

The circumference of a circle is to the perimeter
of the circumscribed square, as the area
of the circle is to the area of the square.

That ratio is called  π
4		 .

Again, since π is approximately 3, then just as the circumference is a bit more than three fourths of the perimeter of the square, so the circle will be a bit more than three fourths of the square itself.

What is more, it is possible to prove the following:

π
4		   =  1 −  1
3		   +   1
5		   −   1
7		   +   1
9		   −    1 
11		   +   .  .  .
If   π
4		   were equal to just 1, that would mean that the circle is equal

to the square.

If   π
4		   were equal to 1 −  1
3		 , that would mean that the circle is equal

to the square, minus a third of the square.  And so on.  

If there is anything in mathematics that deserves to be called beautiful, it is here.  We find such beauty especially when geometry is reflected in arithmetic.  Moreover, we discover these relationships in those archetypal forms; we do not invent them.