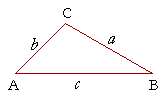
4 Definitions of the Trigonometric Functions BEFORE DEFINING THE TRIGONOMETRIC FUNCTIONS, we must see how to relate the angles and sides of a right triangle. 
A right triangle is composed of a right angle, the angle at C, and two acute angles, which are angles less than a right angle. It is conventional to label the acute angles with Greek letters. Let us label the angle at B with the letter θ ("THAY-ta"). And let us label the angle at A with the letter φ ("fie"). Now, the side AB, opposite the right angle, is called the hypotenuse ("hy-POT'n-yoos"). Each acute angle is formed by the hypotenuse and the side adjacent to the angle. Thus, angle θ is formed by the hypotenuse and side BC. Angle φ is formed by the hypotenuse and side AC. With respect to angle θ, though, side AC is its opposite side. While side BC is the side opposite φ. It should be clear that in a right triangle, the relations -- the ratios -- 
of the sides depend only on the acute angle θ. It is possible to form six such ratios: the ratio of the opposite side to the hypotenuse; of the adjacent side to the hypotenuse; and so on. Those six ratios have historical names and abbreviations, with which the student will have to make peace. They are the following. 
Notice that each ratio (function) in the right-hand column is the inverse ratio, or the reciprocal, of the ratio in the left-hand column. The reciprocal of sin θ is csc θ ; and vice-versa. The reciprocal of cos θ is sec θ. And the reciprocal of tan θ is cot θ. As for why these are called functions, we say that one quantity is a "function" of another if the first depends on the other. For example, the circumference of a circle is a function of the radius, because the size of the circumference depends on the size of the radius. And so we call these trigonometric functions rather than just trigonometric ratios, because each ratio, as we will see, depends on the acute angle. Problem 1. Complete the following with either "opposite," "adjacent to," or "hypotenuse." To see the answer, pass your mouse over the colored area. 
a) In a right triangle, the side opposite the right angle is called the a) hypotenuse. b) CA is called the side opposite angle θ. c) BC is called the side adjacent to angle θ. d) AC is called the side adjacent to angle φ. e) BC is called the side opposite angle φ.
Problem 2. The sides of a right triangle are in the ratio 3:4:5, as shown. Name and evaluate the six trigonometric functions of angle θ.
Problem 3. The sides of a right triangle are in the ratio 8 : 15 : 17, as shown. Name and evaluate the six trigonometric functions of angle φ.
Notice that the sides of this triangle satisfy, as they must, the Pythagorean theorem:
Problem 4. The height of a triangle. Every triangle, right-angled or not, will have at least two acute angles. 
Let them be the base angles at A and B. And call the base c. Then the height h drawn to that base will cut the entire triangle into two right triangles. Let x be the segment of the base containing the angle A. Then the remaining segment is the difference between the whole c and that segment: c − x. Show that the height h is
In the right triangle containing the acute angle A,
In the right triangle containing the acute angle B,
On substituting the expression for x from line (1), c − h cot A = h cot B, which implies c = h cot A + h cot B = h(cot A + cot B). Therefore, on solving for h,
Problem 5. The area of a triangle. Prove: The area of a triangle is equal to one-half the sine of any angle times the product of the two sides that make the angle.
Specifically, prove that Area of triangle ABC = ½ sin A bc = ½ bc sin A.
The area of a triangle is equal to one-half the base times the height. In triangle ABC, let the base be c. Then Area = ½ ch. Now, sin A = h/b, so that h = b sin A. Therefore, in the expression for the Area, on replacing h with b sin A: Area = ½ cb sin A. Next Topic: Trigonometry of right triangles Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||