Geometric representation
In a right triangle the square drawn on the side opposite
the right angle is equal to the squares drawn on the sides that make
the right angle.
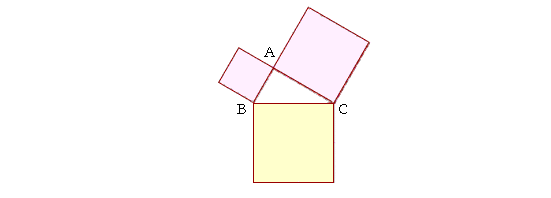
This means that if ABC is a right triangle with the right angle at A, then the square drawn on BC opposite the right angle, is equal to the two squares together on CA, AB.
In other words, if it takes one can of paint to paint the square on BC, then it will also take exactly one can to paint the other two squares.
This is how the sides of a right triangle are related -- by the squares drawn on them -- and we can easily illustrate it with numbers.
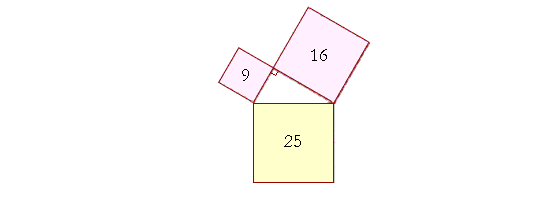
The square drawn on the side opposite the right angle, 25, is equal to the squares on the sides that make the right angle: 9 + 16.
The side opposite the right angle is called the hypotenuse ("hy-POT'n-yoos"; which literally means stretching under).
We will indicate the right angle by a small square.
As for the sides themselves, they will be the square roots. That is, when the squares are 9, 16, 25, then the sides will be 3, 4, 5. (The square root of 9 is 3; the square root of 16 is 4; and the square root of 25 is 5. See Topic 2: Radicals.)
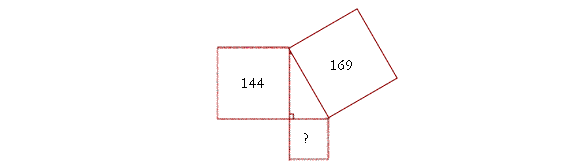
Problem 1. How big is the remaining square? And how long are the sides of the triangle?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
The square drawn on the hypotenuse is 169 square inches, say. Therefore, the remaining square is 169 − 144 = 25 square inches.
144 + 25 = 169.
As for the sides, they will be the square roots: 12, 5, 13.
12² + 5² = 13²
Problem 2. How big is the remaining square? And how long are the sides of the triangle?
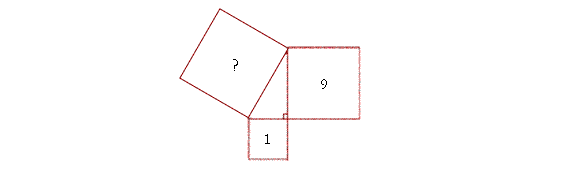
Here, the hypotenuse is unknown. We have 9 + 1 = 10.
As for the sides, the square root of 9 is 3. The square root of 1 is 1. And the square root of 10 is just that -- 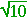 .
.
The sides are 3, 1, 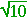 .
.
Algebraic representation
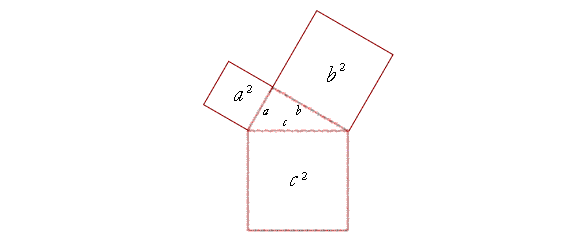
Algebraically, if the hypotenuse is c, and the sides are a, b, then
c² = a² + b².
Example 1. How long is the unknown side x?
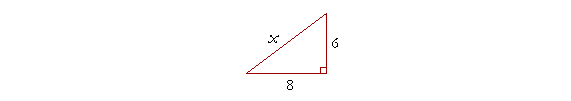
Answer. Here, the hypotenuse is unknown. We have
x² = 8² + 6²
x² = 64 + 36
x² = 100.
Therefore,
x = 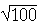 = 10.
= 10.
Example 2. How long is the unknown side x?
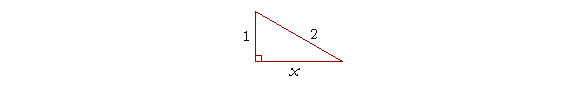
Answer. Here, the unknown is not the hypotenuse but a side.
x² + 1² = 2²
x² = 4 − 1 = 3./P>
Therefore,
x = 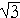 .
.
Problem. In each figure, is the unknown length x the hypotenuse or a side? In each case, find the unknown length x.
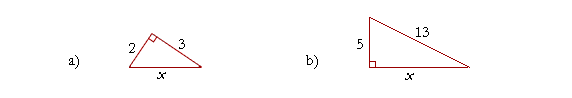
A proof of the Pythagorean theorem
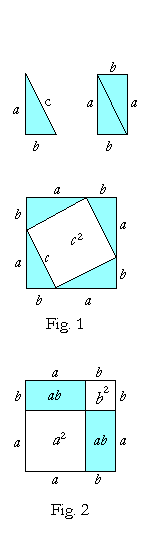
Let a right triangle have sides a, b, and hypotenuse c. And let us arrange four of those triangles to form a square whose side is a + b. (Fig. 1)
Now, the area of that square is equal to the sum of the four triangles, plus the interior square whose side is c.
Two of those triangles taken together, however, are equal to a rectangle whose sides are a, b. The
area of such a rectangle is a times b: ab. Therefore the four triangles together are equal to two such
rectangles. Their area is 2ab.
As for the square whose side is c, its area is simply c². Therefore, the area of the entire square is
c² + 2ab. . . . . . . (1)
At the same time, an equal square with side a + b (Fig. 2) is made up of a square whose side is a, a square whose side is b, and two rectangles whose sides are a, b. Therefore the area of that square is
a² + b² + 2ab.
But this is equal to the square formed by the triangles, line (1):
a² + b² + 2ab = c² + 2ab.
Therefore, on subtracting the two rectangles -- 2ab -- from each square, we are left with
a² + b² = c².
This is the Pythagorean theorem!
Next Topic: The Definitions of the Trigonometric Functions (Ratios)
The Topics | Home
www.proyectosalonhogar.com