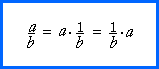2 Radicals: Rational and Irrational Numbers Rational and irrational numbers IN THIS TOPIC we will develop some elementary techniques that are used in trigonometry. First, we must learn about the "square numbers." The square numbers are the numbers 1· 1, 2· 2, 3· 3, and so on. The following are the first ten square numbers and their roots.
The square root of 1 is 1. The square root of 4 is 2. The square root of 9 is 3. And so on. We write
"The square root of 25 is 5." This mark Problem 1. Evaluate the following. To see the answer, pass your mouse over the colored area. a) The fundamental algebraic property of the square root radical is the following:
A radical multiplied by itself produces the radicand. Problem 2. Evaluate the following. a) Example 1. Solve this equation:
Example 2. Solve this equation:
Because ( In other words, if an equation looks like this:
We often use the double sign ± ("plus or minus") and write:
Problem 3. Solve for x. a) x² = 9
x = ±3
b) x² = 8
x = ± Rational and Irrational Numbers A rational number is any whole number, any fraction, any mixed number, or any decimal; positive, negative, or 0. The rational numbers are the ordinary knowable numbers of arithmetic. That is what a rational number is. As for what it looks
integers (b ≠ 0). Problem 4. Which of the following numbers are rational?
All of them! An example of a number that is not rational is
(The wavy equal sign means "is approximately".) How could we know that? By multiplying 1.414 by itself. If we do, we get 1.999396 -- which is almost 2. It should be clear that no decimal multiplied by itself can ever be exactly 2.00000000000000. Because if the decimal ends in 1, then its square will end in 1. If the decimal ends it 2, its square will end in 4. And so on. No decimal -- no rational number -- multiplied by itself can ever produce 2. Therefore, Which square roots are rational and which are irrational? Only the square roots of square numbers are rational. All the rest are irrational.
And so on. The rational numbers together with the irrational numbers are called the real numbers. To learn about the evolution of the real numbers starting with the natural numbers, click here. Rationalize a denominator Rationalizing a denominator is a simple technique for changing an irrational denominator into a rational one. We simply multiply the radical by itself -- but then we must multiply the numerator by the same number. (See Skill in Algebra: Equivalent fractions.)
Solution. Multiply both the numerator and denominator by 
The denominator is now rational.
reciprocal of the denominator:
(In algebra, that is called the definition of division.)
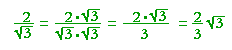
Multiply radicals Multiply radicals as follows:
Problem 6.
a) Next Topic: The Pythagorean Theorem Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||