Natural numbers: cardinal and ordinal
The natural numbers are the counting numbers. They have two forms, cardinal and ordinal. The cardinal forms are
One, two, three, four, etc.
They answer the question How much? or How many?. The ordinal forms are
First, second, third, fourth,
etc.
They answer the question Which one?.
Parts of natural numbers
We say that a smaller number is a part of a larger number if the larger number is a multiple of the smaller.
Here are the multiples of 5:
5, 10, 15, 20, 25, 30, etc.
5 is the first multiple of 5. 10 is the second multiple; 15, the third; and so on.
5 is a part of each one of those (except itself). Since 15, for example, is the third multiple of 5, we say that 5 is the third part of 15. We use that same ordinal number to name the part.
Similarly, 5 is the fourth part of 20. It is the fifth part of 25; the sixth part of 30. And so on.
5 is which part of 10? We do not say the second part. We say half. 5 is half of 10.
It is important to understand that we are not speaking here of proper fractions -- numbers that are less than 1, and that we use for measuring. We are explaining how the ordinal numbers -- third, fourth, fifth, etc. -- name the parts of the cardinal numbers. We will come to those fractional symbols shortly.
Note that 5 is not a part of itself. There is no such thing as the first part.
So, with the exception of the name half, the parts are named with ordinal numbers. Each ordinal number tells which part.
(See Skill in Arithmetic, Lesson 14.)
Problem 1. 7 is which part of 28?
The fourth.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Problem 2. Which part of 45 is 9?
The fifth.
Problem 3. 6 is which part of 12?
Half.
Problem 4. What number is the eighth part of 24?
3
Problem 5. 3 is the tenth part of what number?
30
Parts, plural
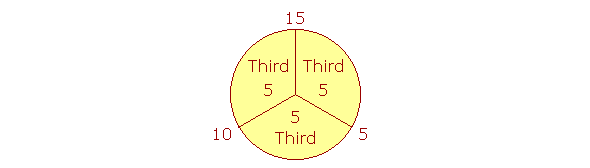
The figure shows that each 5 is a third part of 15, and so we say that 15 has been divided into thirds, that is, into three equal pieces.
5, 10, 15.
Therefore, 10 -- which is two 5's -- is two third parts of 15. One third. Two thirds.
Now, 10 is not a part of 15, because 15 is not a multiple of 10. We say that it is parts, plural: Two third parts, or simply two thirds. Those words are to be taken literally.
Similarly, if we divide 15 into its fifths,

then
3 is the fifth part of 15.
6 is two fifth parts of 15.
9 is three fifth parts of 15. (Count them!)
12 is four fifth parts of 15, or simply four fifths.
And 15 is all five of its fifth parts.
The ratio of natural numbers
Definition. The ratio of two natural numbers is their relationship with respect to relative size which we can express in words. Specifically, it is their relationship in which one number is a multiple of the other (so many times it), a part of it, or parts of it.
(Skill in Arithmetic, Lesson 16.)
Example 1. Multiple What ratio has 15 to 5?
Answer. 15 is three times 5.
That is the ratio -- the relationship -- of 15 to 5.
We do not answer "3 to 1," because we want to name the ratio of 15 to 5 explicitly. It is true that 15 is to 5 in the same ratio as 3 is to 1. 3 is three times 1, just as 15 is three times 5.
The two numbers in a ratio are called the terms; the first term and the second.
Notice that we answer with a complete sentence beginning with the first term: "15 is three times 5." For, a ratio is a relationship.
Example 2. Part What ratio has 5 to 15?
Answer. 5 is the third part of 15.
That is the inverse ratio of 15 to 5. The terms are exchanged.
Example 3. Parts What ratio has 10 to 15?
Answer. 10 is two thirds of 15.
These are the three types of ratio: One number is a multiple of the other -- so many times it -- a part of it, or parts of it.
Problem 6. What ratio have the following? Answer with a complete sentence beginning with the first term.
a) 2 to 10?
2 is the fifth part of 10.
is called "one-third" because of the ratio of 1 to 3. 1 is one third of 3.
Fractional symbols may therefore be regarded as ratio symbols, in that they signify the ratio of the numerator to the denominator.
1 is to 2 as 2 is to 4 as 5 is to 10, etc.
Proportions
A proportion is a statement that two ratios are the same.
5 is to 15 as 8 is to 24.
5 is the third part of 15, just as 8 is the third part of 24.
We will now introduce this symbol 5 : 15 to signify the ratio of 5 to 15. A proportion will then
appear as follows:
5 : 15 = 8 : 24
"5 is to 15 as 8 is to 24."
Example 5. 12 : 2 = 42 : 7. ("12 is to 2 as 42 is to 7.")
Why is this a proportion?
Answer. Because 12 is six times 2, just as 42 is six times 7.
Problem 8. Complete this proportion, 3 : 12 = 7 : ?
28. 3 is the fourth part of 12, and 7 is the fourth part of 28.
The theorem of the alternate proportion
The numbers in a proportion are called the terms: the 1st, the 2nd, the 3rd, and the 4th.
1st : 2nd = 3rd : 4th
We say that the 1st and the 3rd are corresponding terms, as are the 2nd and the 4th.
The following is the theorem of the alternate proportion:
If four numbers are proportional,
then the corresponding terms are also proportional. That is, as the first term
is to the third, so the second will be
to the fourth.
|
| If |
| |
a : b = m : n, |
| then, alternately, |
| |
a : m = b : n. |
Since
1 : 3 = 5 : 15,
then alternately,
1 : 5 = 3 : 15.
(Skill in Arithmetic: Lesson 17, Question 2.)
The theorem of the same multiple
Let us complete this proportion,
4 : 5 = 12 : ?
| Now, 4 is four fifths of 5 (" |
4
5 |
") |
, but it is not obvious of what number |
12 is four fifths.
Alternately, however, 4 is a third of 12 -- or we could say that 4 has been multiplied by 3. Therefore 5 also must be multiplied by 3,
4 : 5 = 12 : 15
That is,
4 : 5 = 3 × 4 : 3 × 5
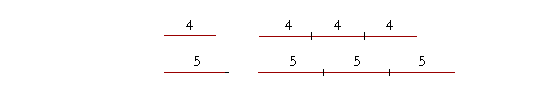
As one 4 is to one 5, so any number of 4's will be to an equal number of 5's. Three 4's are four fifths of three 5's.
The theorem of the same multiple implies that, inversely, we may divide both terms by the same number.
(As for the method of cross-multiplying, that is an algebraic method which is taught in order to avoid teaching ratio and proportion verbally. It stems from a 19th century resistance to language in mathematics.)
Similar figures
Geometry is the study of figures.
Similar figures are equiangular, and the sides that make the equal angles are proportional.
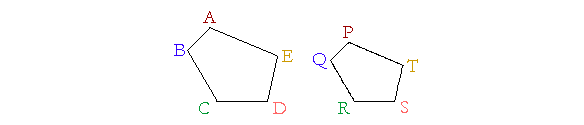
Thus, to say that figures ABCDE, PQRST are similar, is to say that the angle at A is equal to the angle at P, the angle at B is equal to the angle at Q, etc.; and, proportionally, as AB is to BC, so PQ is to QR.
And so on, for each pair of equal angles and the sides that make them.
Example 10. Let triangles HJK, LMN be similar, and let HJ = 2 in, HK = 4 in, and JK = 5 in. How long are LN and MN?
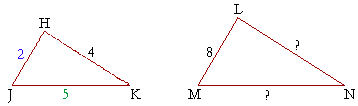
Answer. Since HJ is half of HK, then LM will also be half of LN. Therefore, LN is 16 in.
Next, since HJ is two fifths of JK, then LM is also two fifths of MN: 8 is two fifths of 20.
How to know that? 8 is 4 × 2. And 4 × 5 is 20.
Example 11. In the similar triangles below, let HJ = 3 cm, JK = 5 cm, KH = 4 cm, and LM = 6 cm. How long are MN and LN?
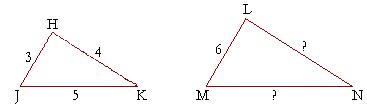
Answer. We have
HJ : JK = LM : MN
and therefore, alternately,
HJ : LM = JK : MN.
That is
3 : 6 = 5 : 10.
MN = 10 cm.
Similarly, LN will be twice as long as HK. LN will be 8 cm.
In other words, since the side corresponding to HJ has been multiplied by 2, every side will be multiplied by 2. This is the theorem of the same multiple.
Problem 13. Triangles ABC, DEF are similar.
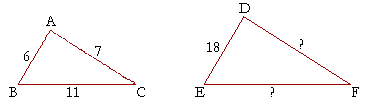
AB = 6 cm, BC = 11 cm, CA = 7 in, and DE = 18 cm. How long are DF and EF?
The side corresponding to AB has been multiplied by 3. Therefore every side will be multiplied by 3. DF = 21 cm, and EF = 33 cm.
Next Topic: Radicals: Rational and Irrational Numbers
The Topics | Home
www.proyectosalonhogar.com