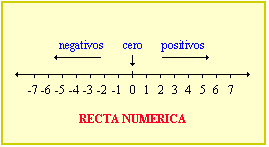
| Para indicar si un objeto se encuentra
a la derecha o a la izquierda de un punto de referencia, podemos indicar
con un signo + si está hacia la derecha y con un signo - si se ubica
hacia la izquierda. De esta forma obtenemos dos conjuntos: |
- Conjunto de números
positivos
- Conjunto de
números
negativos |
| El conjunto formado por los números positivos,
los números negativos y el cero
se llama conjunto de números
enteros. |
 |
|
|
|
|
|
|
|
Sumas
y restas entre
números
enteros
|
|
Los
comerciantes europeos usaban los signos "+"
y "-" para diferenciar las ganancias de
las pérdidas o deudas.
De allí
fue que los matemáticos adoptaron estos signos y,
comenzaron a escribir 5 + 10 en vez de

Esto era lo que se usaba antes de usarse el signo "+" :
"p'' era el símbolo de la suma, pues la palabra "plus''
significa en latín "más''. Así, cuando en Europa se
comenzaron a usar los
números que
representaban deudas, se les asignó el signo "-''
adelante. |
|
Se comenzará por observar que una resta entre
números
naturales puede interpretarse de la siguiente manera,
usando los
números
negativos:
Si se
piensa que el número negativo -6 representa una deuda en
bolívares, está claro que al tener 10 Bs. más una deuda
de 6 Bs., el saldo es de 4 Bs., y esto es lo que se
obtiene al restar 10 -6.
Así,
siempre que se tenga que realizar una resta , puede
escribirse como la suma del minuendo más el opuesto del
sustraendo.
|
|
|
|
En esta operación última la resta podría parecer un poco
extraña: un número negativo menos un número positivo. Si
la escribimos como suma del minuendo más el opuesto del
sustraendo, se obtiene una suma de
dos
números negativos.
Podría decirse, la suma de dos deudas. Ciertamente, eso
lo que da es una deuda mayor que las anteriores.
¿Exactamente a cuánto alcanza la deuda?
|
|
Naturalmente, se suman 20+37=57 y eso da la cantidad que
se debe, es decir,
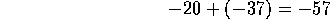
|
|
Veamos ahora este
caso:
|
|
|
En este
caso, debe restarse a 30 un número mayor, que es 40. Si
se interpreta como la suma de 30 + (-40) , se puede
realizar esa operación, cosa que no podía hacerse cuando
no se conocían los
números negativos.
Volviendo a pensar en deudas, se tiene 30 Bs. y una
deuda de 40 Bs. Eso significa que se paga lo que se
tiene y se siguen debiendo 10 Bs.
Es decir:

Ahora se sabe que cualquier resta se puede interpretar
como una suma (el minuendo más el opuesto del
sustraendo). Bastará entonces con aprender bien a
realizar la SUMA de
números
enteros,
para poder realizar cualquier suma o resta de
números
enteros.
Como los
números
enteros
pueden ser positivos o negativos, se estudiarán los
casos que es posible encontrar:
|
Suma
de dos
enteros
positivos:
Se realiza
como hasta ahora se han sumado dos
números
naturales:

|
|
Suma de dos
enteros de
signos contrarios:
Cuando se suman
dos
números de signos
contrarios, se está en presencia de una ganancia y una
pérdida; se sabe bien que si la pérdida es mayor que la
ganancia, lo que queda al final es una deuda, y si, por
el contrario, la ganancia es mayor que la pérdida, lo
que queda es ganancia.
De esta
manera, se ve que el signo del resultado de sumar dos
números de
signos contrarios es el signo del mayor de los
números, si
ambos fueran positivos. |

|
|
|
|
Podría interpretarse la suma del ejemplo como la
operación de "moverse" 8 unidades a la derecha de -10.
Se puede ver que, como 8 es menor que 10, al moverse uno
8 unidades a la derecha, no alcanza al cero. Faltarían 2
unidades para alcanzar al cero. Es decir, se llega hasta
-2.
|
 |
El monto total de pérdida
o ganancia en cada caso será la diferencia
entre los
números,
ignorando el signo.
|
| |
En el ejemplo 5: -10+8=-2 porque la
diferencia entre 10 y 8
es 2.
|
|
|
En el ejemplo 6: 11+(-8)=3 porque la
diferencia entre 11 y 8
es 3.
|
|
|
De nuevo, puede interpretarse esta suma como el
resultado de moverse desde 11, hacia la izquierda, 8
unidades.
Otros ejemplos:
|
-5+7=2 |
|
|
3+(-1)=2 |
|
|
9+(-12)=-3
|
|
|
|
En los ejemplos citados al comienzo, se tienen sumas de
números con
signos contrarios.
Se tiene

El resultado 9, lleva el signo positivo porque 12 tiene
signo positivo. En 2), igualmente tenemos
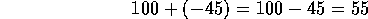
En cambio, en 4), el mayor de los dos
números (sin
tomar en cuenta el signo) entre 30 y (-40) es 40.
En la suma original, tiene signo negativo, por lo tanto,
al restar 40-30, para efectuar esa suma, debemos
colocarle el signo negativo al resultado.

|
|
Si has
acertado en todas tus respuestas, ¡felicitaciones! has
hecho un buen avance, y eso te permitirá seguir
aprendiendo lo que sigue sin dificultades.
Si no has
realizado correctamente alguno de los ejercicios, revisa
de nuevo los ejemplos que se han dado antes, para que
asimiles mejor las ideas expuestas. |
|
Suma de dos
enteros
negativos:
Si tenemos
que sumar, por ejemplo, -9 + (-3) , ya sabemos que la
suma de dos deudas es una deuda, en este caso igual a:

Veamos otros ejemplos:
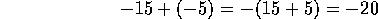
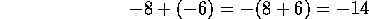
Hemos
dicho antes que el opuesto de un número entero es aquel
que, sumado a nuestro número, nos da el cero:
|
El opuesto de 5 es -5, pues 5 + (-5) = 0
El opuesto de 3 es -3, pues 3+ ( -3) = 0
El opuesto de -7 es 7, pues -7 + 7 = 0
El opuesto de -1 es 1, pues -1+1 = 0
|
|
|
Es claro que dado cualquier entero positivo, para
encontrar su opuesto, basta con anexarle un signo - por
delante. Por ejemplo: el opuesto de 8 es -8.
El signo
-, delante de cualquier expresión matemática, significa
el opuesto de esa expresión. Por
ejemplo: el opuesto de -6 es -(-6)=+6.
Por otra
parte, como se acaba de ver en los ejemplos anteriores,
para encontrar el opuesto de un número negativo, basta
con eliminar el signo - del número. Por ejemplo: el
opuesto de -9 es 9.
Viendo
estas cosas desde el punto de vista de las deudas y las
ganancias, es natural pensar que lo opuesto de una deuda
es una ganancia de esa misma magnitud:



Es muy importante tener presente lo que cada símbolo
matemático significa. Aprender Matemáticas se parece a
aprender un idioma nuevo. Si no se comprende lo que
significa cada palabra de una frase, no se puede
entender la frase.
Entre los
símbolos importantes en el lenguaje de las matemáticas
está el signo -. Como se dijo antes, no debe olvidarse
su significado: se usa para expresar el opuesto de
cualquier expresión que le siga.
Si se
quiere calcular lo siguiente:

Aquí es importante decir que el paréntesis sirve para
especificar lo siguiente: todo lo que está
dentro del paréntesis está afectado por
el signo negativo. Si se tiene en cuenta el
significado de esa expresión matemática, no habrá
dificultad alguna, pues basta con calcular lo que está
dentro del paréntesis, y luego encontrar su opuesto,
porque eso es lo que indica el signo - delante de todo.
Entonces,
76+32=108, y el opuesto de 108 es -108, por lo tanto,
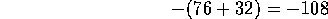
|
|
Otros
ejemplos:
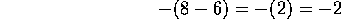
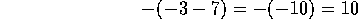
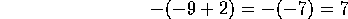
Ahora, ocurre algo muy simpático con estos ejemplos, y
es que se pueden hacer los cálculos de otra manera y
obtener el mismo resultado. Con mucha frecuencia en
Matemáticas ocurre esto: hay más de una forma correcta
de resolver los problemas y ejercicios.
Se verá
cuál es esa otra forma en este caso. En el primer
ejemplo,

en lugar de calcular, como se hizo antes, en primer
lugar lo que está dentro del paréntesis, es posible
deshacerse del paréntesis primero, haciendo "entrar" al
signo -, permitiéndole actuar sobre cada número, así:
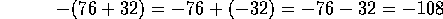
El signo -, al entrar en la expresión dentro del
paréntesis, se coloca delante de cada número que
encuentra a su paso, y luego se realizan las operaciones
indicadas.
Se
calcularán los otros ejemplos, haciéndolo de esta misma
manera:
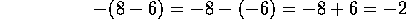
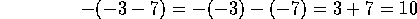
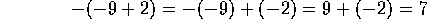
|
|
Signos de agrupación
Algunas
veces se hace necesario realizar operaciones de suma y
resta con más de dos
números
enteros,
por ejemplo:
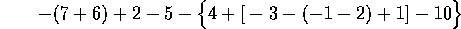
Los signos
 (paréntesis),
(paréntesis),
 (corchetes) y
(corchetes) y
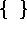 (llaves) son llamados signos de agrupación y su papel en
las expresiones como la anterior, es el mismo que el de
los paréntesis, explicado ya.
(llaves) son llamados signos de agrupación y su papel en
las expresiones como la anterior, es el mismo que el de
los paréntesis, explicado ya.
La
diferencia entre un signo de agrupación y otro es sólo
que se usan en este orden: el más interno: paréntesis,
luego viene el corchete, y el más externo es la llave.
Un signo -
delante de un paréntesis o de un corchete, o de una
llave, indica que se tomará el opuesto de todo lo que
hay dentro del signo de agrupación.
Deberán,
entonces, realizarse las operaciones que están dentro de
cada signo de agrupación y luego cambiarse el signo en
este caso.
Si el
paréntesis, el corchete o la llave están precedidos por
un signo +, no se cambia el signo de lo que está dentro
de los signos de agrupación.
Para
realizar la operación anterior, se comienza por operar
con lo que hay dentro de los signos de agrupación más
internos: los paréntesis.

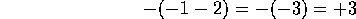
Así la expresión
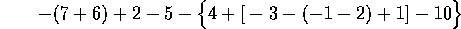
se transforma en
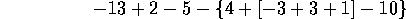
Ahora se calcula lo que hay dentro de los corchetes:
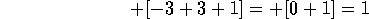
y se escribe
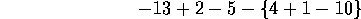
Resolviendo las operaciones dentro de las llaves, se
obtiene
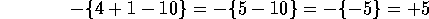
y así la expresión original es igual a
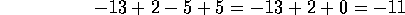
|
| |
| |
|
Bibliografía utilizada:
Sotelo, M. (1987) Historia de
Los
Números.
Caracas: Editorial Algoritmo. |
|
Fundación Educativa
Héctor A. García |