S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

THE MEANING OF SUBTRACTION

Mental Arithmetic

Lesson 6  Section 2

Subtract by the ending

Knowing the endings in addition (Lesson 4) becomes skill in subtraction. For example, to find the number we must add to 8 to get 32 --

328

-- let us ask:

8 + ?  ends in 2?

8 + 4 ends in 2 -- because 8 + 4 is 12.

Therefore,  328  will also end in 4.  It must be 24.  The answer falls in the previous decade.

In fact, whenever we take an 8 from a 2, the answer always ends in 4.

428 = 34

628 = 54

928 = 84

The answers fall in the previous decade.  These are problems you should not have to write down.  

Example 1.   419

Solution.   9 + ?  ends in 1.

Solution.   9 + 2 ends in 1,  because 9 + 2 is 11.  Therefore,

419 = 32

Example 2.   You could know

848 = 76,

because 8 + 6 ends in 4.

To summarize:
 3.   How can we find the difference by the ending?
 
84 − 8 = 76
 
  Decide what number you must add to the smaller number to get the ones digit of the larger.
 

The difference between two-digit numbers

First:
 4.   How can we subtract a number in the previous decade?
9287
 
  Add to the smaller number to complete a 10. Then add the ones of the larger.
"87 plus 3 is 90, plus 2 is 92."
 
92 − 87 = 5
 

Example 3.   52 − 46

Say only, "4 + 2 is 6."

That is, 46 plus 4 is 50,  plus 2 is 52.


Example 4.   57 + ? = 65

"3 + 5 is 8."

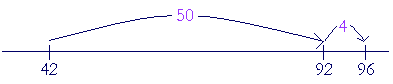
Example 5.   2318

"2 + 3 is 5."

These are problems that you should not have to write, and certainly should not require a calculator.

Next, let's look at two-digit numbers that are farther apart.

42 + ? = 96

How to do it?  First add enough tens to get to the 90's.

"42 + 50 is 92, plus 4 is 96."

42 + 54 = 96.

   Example 6.    25 + ? = 87
 
  "25 + 60 is 85, plus 2 is 87."

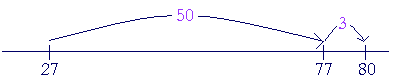
That is,  25 + 62 = 87.

Finally, here is the case where the ones digit of the smaller number is greater.

27 + ? = 80

First consider the case where we're going to a multiple of 10.  In this case, add to get to the previous decade -- the 70's.

"27 plus 50 is 77, plus 3 is 80."

27 + 53 = 80.

In practice, say only,

"50 + 3 is 53."

   Example 7.    36 + ? = 90
 
  "50 plus 4 is 54."
 
That is,   36 + 50 is 86, plus 4 is 90."
   Example 8.    38 + ? = 60
 
  "20 plus 2 is 22."

(38 plus + 20 is 58, plus 2 is 60.)

Now say that the larger number is not a multiple of 10.

38 + ? = 64

Again, add to 38 to get to the previous decade. But in this case we know that the difference will end in 6 -- the ones digit will be a 6.  (8 + 6 ends in 4.)

38 + 26 = 64.

38 plus 20 is 58, plus 6 is 64.

To summarize:


 5.   How can we find the difference of two-digit numbers when the ones digit of the smaller number is greater?
23 + ? = 61
 
  Decide how the difference will end. Then add
to get to the previous decade.

Example 9.   23 + ? = 61

Solution.  The difference will end in 8.  (3 + 8 ends in 1.)  Therefore,

23 + 38 = 61.

(23 plus 30 is 53, plus 8 is 61.)

   Example 10.    55 + ? = 82
 
  "55 + 20 is 75.  27."

The difference ends in 7.

At this point, please "turn" the page and do some Problems.

or

Continue on to the next Section.

Section 1 of this Lesson


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com