S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

THE MEANING OF SUBTRACTION

Mental Arithmetic

Lesson 6  Section 3


Problem.   If an item costs $.79 and you give a dollar bill, how much is your change?

Answer.  What must you add to $.79 to get $1.00?

.79 + .21 = 1.00

("79 + 20 = 99; plus 1 is 100.")

Your change is 21¢.

In other words,
 6.   How do we complete 100?
64 + ? = 100
  Add tens to get into the 90's, then add ones to complete 100.

Example 1.   64 + ? = 100

 Solution.   We must get into the 90's.  64 + 30 brings us to 94.  Plus 6 is 100.

64 + 36 = 100

36 is called the complement to 100 of 64, because 36 completes 64 to make 100.

Notice that the tens digits, 6 + 3, add up to 9 tens -- they bring us to the 90's.  While the ones digits, 4 + 6, add up to 10.

Example 2.   In a recent election, 58% voted for Smith.  What percent did not vote for Smith?

Answer.  100% is the whole. (Lesson 3, Question 7.)  So the question is,

58 + ? = 100

58 + 40 brings us to 98.   Plus 2 is 100.

42% did not vote for Smith.

Again, the tens digits, 5 + 4, add up to 9 tens -- that brings us to the 90's; while the ones digits, 8 + 2, add up to 10.

Example 3.   How much is 10486?

Technique.  First, complete 100:

86 + 14 will bring us to 100.  Plus 4 is 104.

Thus the distance between 86 and 104 is

14 + 4 = 18.

Example 4.   Mark Twain was born in 1835 and died in 1910.  How old was he when he died?

Answer.  Jump first to the century mark.  Say,

"1835 plus 65 is 1900, plus 10 is 1910.  He was 75."   (65 + 10)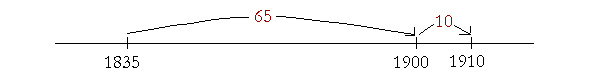

Example 5.   How many years passed between the discovery of America in 1492 and the signing of the Declaration of Independence in 1776?

Solution.  What must we add to 1492 to get 1776?

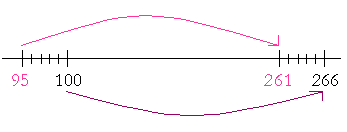
1492 + 200 brings us to 1692.  Plus 8 is 1700.  Plus 76 is 1776.

208 + 76 = 284 years


Rounding off

261 − 95

The following is a basic property of subtraction:

If we add the same number to both the smaller and the larger,
the difference will not change.

Why?  Because their difference is the distance between them.

If we add 5 -- or any number -- to both 95 and 261, the distance between them does not change. Therefore,

261 − 95 = 266 − 100 = 166.
 7.   How do we subtract by rounding off?
 
  75 − 18 = 77 − 20 = 57
 
  Add to the smaller number to make it a multiple
of 10. To compensate, add that same number to the larger.
Or, subtract and then add that same number to the answer.

Example 6.    67419

Round off 19 to 20 by adding 1.  Compensate by adding 1 to 674. Say,

Example 6.   "67520 = 655."

Example 7.    8538

Add 2 to both numbers.

Example 7.   "8740 = 47."


Or, if we add only to 38, then

Example 7.   "8540 = 45,  plus 2 is 47."

Example 8.   The cents in the smaller number are less.

8.733.29

29 cents is less than 73 cents.  In this case, subtract the cents first.  Round off to 30 cents and say,

"74 minus 30 is 44.   5.44."

(83 = 5)

Example 9.   The cents in the smaller number are more.

$48.00 − $15.90

90 cents are more than no cents. In this case, round off to the next whole dollar. Say,

"$48 − $16 is $32,

plus 10 cents is $32.10."

Example 10.   9.102.79

Round off to the next whole dollar -- by adding the complement to 100 of the 79 cents.

"9.10 minus 3.00 is 6.10,

plus 21 cents is 6.31."

21¢ is the complement to 100 of 79¢.

Example 11.   How much is $115 less 10%?

Solution.   10% of $115 is $11.50. (Lesson 3.)  Therefore say,

"$115 minus $12 is $103;

plus 50 cents is $103.50."

Example 12.   You have $374.12 in your checking account, and you write a check for $48.70.  What is your new balance?

Answer.  Speak!   "$374.12 minus 50 dollars is $324.12,

plus $1.30 is $325.42."

Faster than a calculator!


Please "turn" the page and do some Problems.

or

Continue on to the next Lesson.

Section 1 of this Lesson

Section 2


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com