|
Lesson 7 SUBTRACT WHOLE NUMBERS
|
|||||||||||||||||||||
| 8 thousands | + 3 hundreds | + 4 tens | + 7 ones |
| − 5 thousands | − 8 hundreds | − 7 tens | − 2 ones |
| 2 thousands | + 4 hundreds | + 7 tens | + 5 ones |
2 ones from 7 ones are 5 ones. No problem.
But we cannot take 7 tens from 4 tens. Therefore, we add 10 tens to 4 tens, and take 7 from 14. To compensate, we add 1 hundred to 8 in the bottom number -- because 1 hundred is equal to the 10 tens we added to 4. (Lesson 1).
9 hundreds from 13 hundreds are 4 hundreds.
6 thousands from 8 thousands are 2 thousands.
Here is the rule:
| 1. | How do we subtract by compensating? |
| − 8,347 | |
| − 5,872 | |
| −2,475 | |
|
Write the smaller number under the larger, taking care to align the same units. Then, starting with the ones on the right, subtract each digit on the bottom from the corresponding digit on top. If a bottom digit is greater, consider the top digit increased by 10. To compensate, add 1 to the next bottom digit. |
|
| Example 1. | 5,312 |
| − 2,879 | |
| 2,433 | |
"9 from 12 is 3."
"8 from 11 is 3."
"9 from 13 is 4."
"3 from 5 is 2."
The top digits 5312 never change. That is the simplicity of this method. Only a bottom digit might change.
Finally, since subtracting is finding what number to add to the smaller number, the student should always check the answer by adding.
3 + 9 is 12. 3 + 7 is 10, plus 1 is 11. And so on.
| Example 2. | 6,000 |
| −1,926 | |
| 4,074 | |
"6 from 10 is 4."
"3 from 10 is 7."
"10 from 10 is 0."
"2 from 6 is 4."
Example 3. 30.21![]() .86
.86
Solution. The smaller number is .86 Write it on the bottom, and align the decimal points:
| 30.21 |
| .86 |
| 29.35 |
"6 from 11 is 5."
"9 from 12 is 3."
"1 from 10 is 9."
"1 from 3 is 2."
Example 4. 2.1 − .867
Solution. .867 is the smaller number. Write it on the bottom. Align the decimal points.
![]()
Note that we must add 0's onto the right of 2.1 (Lesson 2). Both numbers must have the same number of decimal places.
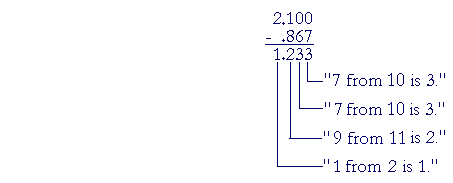
On checking: .867 plus 1.233 is 2. 100.
Example 5. Subtract .698 from 5
Solution. This problem means
5 − .698
.698 is the smaller number. Write it below 5.000:
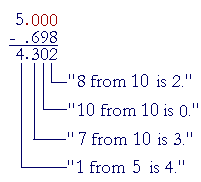
Subtraction with regrouping
| 2. | How do we subtract by regrouping? |
|
|
|
| When a digit in the bottom number is larger, decompose 1 unit of higher value into 10 units of the next lower value, and regroup. | |

We cannot take 6 ones from 2 ones. Therefore, we must decompose 1 of the 4 tens -- break it up -- into 10 ones, and regroup them onto the ones column.

We now have 3 tens and 12 ones. "6 ones from 12 ones are 6 ones."
Next, we cannot take 9 tens from 3 tens. So we decompose 1 of the 5 hundreds into 10 tens, and again regroup. We now have 4 hundreds and 13 tens:

"9 tens from 13 tens are 4 tens."
Finally,

"1 hundred from 4 hundred is 3 hundred."
We can always check the difference 346 by adding it to the smaller number. "6 plus 6 is 12. 4 plus 9 is 13, plus 1 is 14." And so on.
Now, this is the concept of subtraction with regrouping. In actual practice, the student should try not to write the crossings out or the regrouped numbers. The student should practice those steps mentally. The answer can always be checked by adding.
In other words, with practice the student should be able to say:

"6 from 12 is 6."
"9 from 13 is 4."
"1 from 4 is 3."
We will do the following example completely in the expanded form.
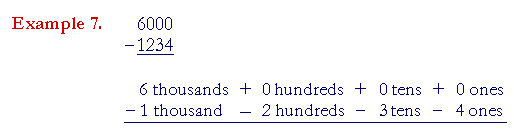
We cannot take 4 ones from 0 ones, and we cannot decompose 0 tens. We must move left and start decomposing at the first place that is not 0, namely 6.
6 is in the thousands place. We will decompose 1 of those thousands into 10 hundreds, and regroup. We now have 5 thousands and 10 hundreds:
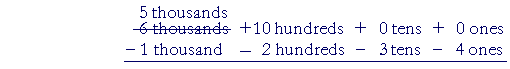
Now we can decompose 1 of the 10 hundreds into 10 tens. That leaves 9 hundreds:
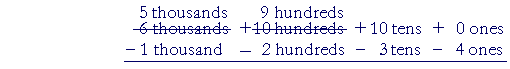
Finally, we can decompose 1 of the 10 tens into 10 ones. That leaves 9 tens:
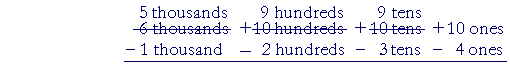
That completes the decomposing and regrouping. The subtraction easily follows:
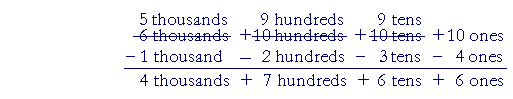
The answer is 4,766.
The problem will appear, of course, like this:
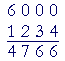
And with practice, the student should be able to say,
"4 from 10 is 6."
"3 from 9 is 6."
"2 from 9 is 7."
"1 from 5 is 4."
Again, we can always check the answer by adding. (Please compare the simplicity of compensating.)
Example 8. Alignment. 68.27![]() 3
3
Answer. 3 is 3 ones. We must subtract it from 8 ones. The answer is 65.27.
As in addition, we must align the digits that have the same place value.
Example 9. Your checking account has a balance of $310.12, and you write a check for $45.24. Then you make a deposit of 126.75, and you write another check for $22.50. What is your present balance?
Answer. Each time you write a check, you must subtract. And each time you make a deposit, you add. Here then is the sequence of subtractions and additions:
| 310.12 | Opening balance | |
| Check | ||
| 264.88 | ||
| + 126.75 | Deposit | |
| 391.63 | ||
| Check | ||
| 369.13 | Present balance | |
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
www.proyectosalonhogar.com
