22
MULTIPLYING AND DIVIDING
ALGEBRAIC FRACTIONS
TO MULTIPLY FRACTIONS, multiply the numerators and multiply the denominators.
![]()
Problem 1. Multiply.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | 2 x |
· | 5 x |
= |
10 x² |
b) | 3ab 4c |
· | 4a²b 5d |
= |
3a³b² 5cd |
The 4's cancel. |
| c) | 3x x + 1 |
· | 6x² x − 1 |
= |
18x³ x² − 1 |
The Difference of Two Squares |
| d) | x − 3 x + 1 |
· | x − 2 x + 1 |
= |
x² − 5x + 6 x² + 2x + 1 |
| In a multiplication of this form a· | b c |
or | b c |
· a, multiply only |
the numerator.
| a· | b c |
= | ab c |
Problem 2. Multiply.
| a) | x |
· | 2x 3 |
= |
2x² 3 |
b) | 3x² 4 |
· 7x3 | = |
|
| c) (x + 3)· | x − 3 x + 6 |
= |
x² − 9 x + 6 |
| d) | x² − 2x + 5 6x² − 4x + 1 |
· 2x3 | = | 6x² − 4x + 1 |
No canceling! |
Canceling
If any numerator has a divisor in common with any denominator,
it may be canceled.
| a b |
· | c d |
· | e a |
= | ce bd |
The a's cancel.
Problem 3. Multiply. Cancel first.
| a) | ab cd |
· | ed fg |
· | hcf ake |
= | bh gk |
| b) | (x − 2)(x + 2) 8x |
· | __2x__ (x + 2)(x − 1) |
= |
x − 2 4(x − 1) |
| c) | __x³__ (x + 2)(x + 3) |
· | x + 3 x7 |
= |
__1_ (x + 2)x4 |
| d) | x(x + 1) 6 |
· | 2 x² − 1 |
= |
x(x + 1) 6 |
· | __2__ (x + 1)(x − 1) |
= |
_x_ 3(x − 1) |
| e) aq· | b cq |
= |
ab c |
f) 10· | x + 2 2 |
= | 5(x + 2) | = 5x + 10 |
| g) 3x· | 5x 6 |
= | 5x² 2 |
| h) | −a b |
· | 1 a |
= | − | 1 b |
| The a's cancel as −1, which on multiplication with 1 makes the fraction itself negative (Lesson 4). |
| Example 1. Multiply | x² − 4x − 5 x² − x − 6 |
· | x² − 5x + 6 x² − 6x + 5 |
Solution. Although the problem says "Multiply," that is the last thing to do in algebra! First factor. Then cancel. Finally, multiply.
And remember: Only factors cancel.
| x² − 4x − 5 x² − x − 6 |
· | x² − 5x + 6 x² − 6x + 5 |
= | (x + 1)(x − 5) (x + 2)(x − 3) |
· | (x − 3)(x − 2) (x − 1)(x − 5) |
||
| = | x + 1 x + 2 |
· | x − 2 x − 1 |
|||||
| = | x² − x − 2 x² + x − 2 |
|||||||
Problem 4. Multiply.
| a) | __x²__ x² + x − 12 |
· | x² − 9 2x6 |
= | __x²__ (x + 4)(x − 3) |
· | (x − 3)(x + 3) 2x6 |
||
| = | 1 x + 4 |
· | x + 3 2x4 |
||||||
| = | _ x + 3 _ 2x5 + 8x4 |
||||||||
| b) | x² − 2x + 1 x² − x − 12 |
· | x² + x − 6 x² − 6x + 5 |
= | __(x − 1)²__ (x − 4)(x + 3) |
· | (x + 3)(x − 2) (x − 1)(x − 5) |
||
| = | x − 1 x − 4 |
· | x − 2 x − 5 |
||||||
| = | x² − 3x + 2 x² − 9x + 20 |
||||||||
| c) | x² + 3x − 10 x² + 4x − 12 |
· | x² + 5x − 6 x² + 4x − 5 |
= | (x + 5)(x − 2) (x + 6)(x − 2) |
· | (x − 1)(x + 6) (x − 1)(x + 5) |
||
| = | 1 | ||||||||
| d) | _x³_ x² − 1 |
· | x² + x − 2 x4 |
· | __x²__ x² + 4x + 4 |
| = | ___x³___ (x + 1)(x − 1) |
· | (x − 1)(x + 2) x4 |
· | __x²__ (x + 2)² |
|||
| = | x + 1 |
· | 1 x + 2 |
|||
| = | _ _x_ _ x² + 3x + 2 |
|||||
Complex fractions: Division
| A complex fraction looks like this: |
The numerator and/or the denominator are themselves fractions.
To deal with a complex fraction, we immediately apply the definition of division (Lesson 6):
| a b |
= a· | 1 b |
Any fraction is equal to the numerator times the reciprocal
of the denominator.
Therefore,
| = | p q |
· | n m |
| Example 2. Simplify | 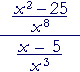 |
| Solution. | 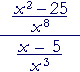 |
= | x² − 25 x8 |
· | x³ x − 5 |
| = | (x + 5)(x − 5) x8 |
· | x³ x − 5 |
|
| = | x + 5 x5 |
|||
Division -- which effectively this is -- becomes multiplication by the reciprocal.
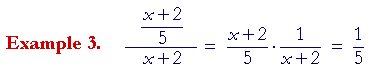
on canceling the x + 2's.
Problem 5. Simplify.
| a) | = |
6 x5 |
· |
x² 8 |
= |
3 4x3 |
| b) | 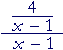 |
= |
4 x − 1 |
· |
1 x − 1 |
= |
_4_ x² − 2x + 1 |
| c) | 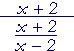 |
= | (x + 2) | · |
x − 2 x + 2 |
= | x − 2 |
| d) | 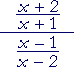 |
= |
x + 2 x + 1 |
· |
x − 2 x − 1 |
= |
x² − 4 x² − 1 |
| e) | 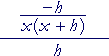 |
= |
−h x(x + h) |
· |
1 h |
= | − |
1 x(x + h) |
The h's cancel. And according to the Rule of Signs, the product is negative. (It's all right to leave the product in its factored form.)
| f) | 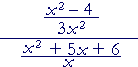 |
= |
(x + 2)(x − 2) 3x² |
· |
_x_ (x + 2)(x + 3) |
| = |
x − 2 3x |
· |
1 x + 3 |
= |
x − 2 3x(x + 3) |
| Example 4. Simplify |
Solution. 1-over any number is its reciprocal. Therefore,
| = | 4 3 |
Problem 6. Simplify the following.
| a) | 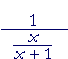 |
= | x + 1 x |
b) | 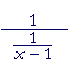 |
= | x − 1 |
Next Lesson: Adding algebraic fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
