Simplifying radicals: Section 2
(If you are not viewing this page with Internet Explorer 6, then your browser may not be able to display the symbol ≥, "is greater than or equal to;" or ≤, "is less than or equal to.")
![]()
We can identify ![]() with the absolute value of x (Lesson 12).
with the absolute value of x (Lesson 12).
![]() .
.
For, when x ≥ 0, then
![]() .
.
But if x < 0 -- if, for example, x = −5 -- then
![]()
![]()
-- because the square root is never negative. (Lesson 26.) Rather, when x < 0, then
![]() .
.
![]() .
.
This conforms to the definition of the absolute value.
Simplifying powers
Example 4. Since the square of any power produces an even exponent -
(a3)² = a6
-- then the square root of an even power will be half the exponent.
![]() = a3
= a3
As for an odd power, such as a7, it is composed of an even power times a:
a7 = a6a
Therefore,
![]() =
= ![]() = a3
= a3![]() .
.
(These results hold only for a ≥ 0.)
Problem 5. Simplify each radical. (Assume a ≥ 0.)
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | b) | c) |
| d) | = | = | a |
e) | ||||||||
| f) | = | = | a7 |
g) | = | = | an |
|||||
Problem 6. Simplify each radical. Remove the even powers. (Assume that the variables do not have negative values.)
| a) | = | 2x |
| b) | = | 2x²y3 |
| c) | = | 3x4yz² |
Factors of the radicand
Problem 7. True or false? That is, which of these is a formal rule of algebra? (Assume that the variables do not have negative values.)
| a) |
True. This is the rule. The square root of a product is the product of the square roots of each factor. |
| b) |
False. The radicand is not made up of factors, as in part a). |
| c) |
False! The radicand is not made up of factors. |
| d) |
True. |
| e) |
True. The radicand is (a + b)². |
Problem 8. Express each radical in simplest form.
a) ![]() =
=
![]() = 2
= 2![]() .
Make factors!
.
Make factors!
b) ![]() =
=
![]() = 2a
= 2a![]()
c) ![]() =
=
![]() = 3b
= 3b![]()
Fractional radicand
A radical is also in it simplest form when the radicand is not a fraction.
Example 5. The denominator a square number. When the denominator is a square number, as ![]() , then
, then
| = | 1 2 |
In general,
![]()
For, a· a = a².
| Example 6.
|
= | The definition of division | ||
| = | 1 2 |
|||
Problem 9. Simplify each radical.
| a) |
1 3 |
b) |
= | 1 3 |
c) |
= | 2 5 |
| d) |
= | 5 6 |
| Example 7. | The denominator not a square number. |
| Simplify | |
Solution. When the denominator is not a square number, we can make it a square number by multiplying it. In this example, we will multiply it by itself, that is, by 2. But then we must multiply the numerator also by 2:
| = | = | = | 1 2 |
Example 8. Simplify ![]() . (Assume that the variables do not have negative values.)
. (Assume that the variables do not have negative values.)
Solution. The denominator must be a perfect square. It must be composed of even powers. Therefore, make the denominator into a product of even powers simply simply by multiplying it -- and the numerator -- by bc. Then extract half of the even powers.
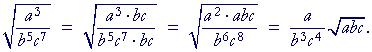
Problem 10. Simplify each radical. (Assume that the variables do not have negative values.)
| a) |
= |
1 3 |
|
b) |
= |
1 5 |
|
c) |
= |
1 7 |
|
| d) |
= | = |
5 6x |
|
| e) |
= |
2 x² |
|
f) |
= |
a² bc² |
|
Next Lesson: Multipying and dividing radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com