28
MULTIPLYING AND DIVIDING
RADICALS
HERE IS THE RULE for multiplying radicals:
![]()
It is the symmetrical version of the rule for simplifying radicals.
Problem 1. Multiply.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | b) 2 |
|||
| c) | = 6 | d) (2 |
||
| e) | The difference of two squares |
Example 1. Multiply (![]() +
+ ![]() )(
)(![]() −
− ![]() ).
).
Solution. The student should recognize the form those factors will produce:
| ( |
= | ( |
| = | 6 − 2 | |
| = | 4 | |
Problem 2. Multiply.
a) (![]() +
+ ![]() )(
)(![]() −
− ![]() ) =
5 − 3 = 2
) =
5 − 3 = 2
b) (2![]() +
+ ![]() )(2
)(2![]() −
− ![]() ) =
4· 3 − 6 = 12 − 6 = 6
) =
4· 3 − 6 = 12 − 6 = 6
c) (1 + ![]() )(1 −
)(1 − ![]() ) =
1 − (x + 1) =
1 − x − 1 =
−x
) =
1 − (x + 1) =
1 − x − 1 =
−x
d) (![]() +
+ ![]() )(
)(![]() −
− ![]() ) =
a − b
) =
a − b
Problem 3. (x − 1 − ![]() )(x − 1 +
)(x − 1 + ![]() )
)
a) What form does that produce?
The difference of two squares. x − 1 is "a." ![]() is "b."
is "b."
b) Multiply out.
| (x − 1 − |
= | (x − 1)² − 2 | ||
| = | x² − 2x + 1 − 2, | on squaring the binomial, | ||
| = | x² − 2x − 1 | |||
Problem 4. Multiply out.
| (x + 3 + |
= | (x + 3)² − 3 |
| = | x² + 6x + 9 − 3 | |
| = | x² + 6x + 6 | |
Dividing radicals
![]()
For example,
| = | = |
Problem 5. Simplify the following.
| a) | = | b) | 8 |
= | 3 4 |
c) | = | a |
= | a· a | = | a² |
Conjugate pairs
The conjugate of a + ![]() is a −
is a − ![]() . They are a conjugate pair.
. They are a conjugate pair.
Example 2. Multiply 6 − ![]() with its conjugate.
with its conjugate.
Solution. The product of a conjugate pair --
(6 − ![]() )(6 +
)(6 + ![]() )
)
-- is the difference of two squares. Therefore,
(6 − ![]() )(6 +
)(6 + ![]() ) = 36 − 2 = 34
) = 36 − 2 = 34
When we multiply a conjugate pair, the radical vanishes and we obtain a rational number.
Problem 6. Multiply each number with its conjugate.
a) x + ![]()
![]() = x² − y
= x² − y
b) 2 − ![]() (2 −
(2 − ![]() )(2 +
)(2 + ![]() ) = 4 − 3 = 1
) = 4 − 3 = 1
| c) |
You should be able to write the product immediately: 6 − 2 = 4. |
d) 4 − ![]() 16 − 5 = 11
16 − 5 = 11
Example 3. Rationalize the denominator:
| 1 |
Solution. Multiply both the denominator and the numerator by the conjugate of the denominator; that is, multiply them by 3 − ![]() .
.
| 1 |
= | 9 − 2 |
= | 7 |
The numerator becomes 3 − ![]() . The denominator becomes the difference of the two squares.
. The denominator becomes the difference of the two squares.
| Example 4. | = | 3 − 4 |
= | −1 |
|
| = | −(3 − 2 |
||||
| = | 2 |
||||
Problem 7. Write out the steps that show the following.
| a) | 1 |
= ½( |
| 1 |
= | 5 − 3 |
= | 2 |
= | ½( |
|
| The definition of division | |||||||
| b) | 2 3 + |
= ½(3 − |
| 2 3 + |
= | 9 − 5 |
= | 4 |
= | ½(3 − |
| c) | _7_ 3 |
= | 6 |
| _7_ 3 |
= | 9· 5 − 3 |
= | 42 |
= | 6 |
| d) | = | 3 + 2 |
| = | 2 − 1 |
= | 2 + 2 |
Perfect square trinomial | |||
| = | 3 + 2 |
||||||
| e) | 1 + |
= | x |
1 + |
= | 1 − (x + 1) |
||||
| = | 1 − x − 1 |
, | Perfect square trinomial | |||
| = | −x |
|||||
| = | x |
on changing all the signs. | ||||
| Example 5. Simplify | 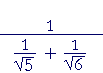 |
| Solution. | 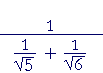 |
= | 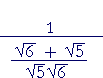 |
on adding those fractions, | |
| = | on taking the reciprocal, | ||||
| = | 6 − 5 |
on multiplying by the conjugate, | |||
| = | 6 |
on multiplying out. | |||
| Problem 8. Simplify | 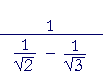 |
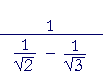 |
= | 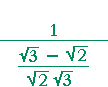 |
on adding those fractions, | ||
| = | on taking the reciprocal, | ||||
| = | 3 − 2 |
on multiplying by the conjugate, | |||
| = | 3 |
on multiplying out. | |||
Problem 9. Here is a problem that Calculus students have to do. Write out the steps that show:
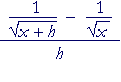 |
= − | ____1____ x |
In this case, you will have to rationalize the numerator.
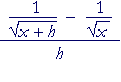 |
= | 1 h |
· | |
| = | 1 h |
· | _____x − (x + h)_____ | |
| = | 1 h |
· | ____x − x − h_____ x | |
| = | 1 h |
· | _______−h_______ x | |
| = | − | _______ 1_______ x | ||
Next Lesson: Rational exponents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
