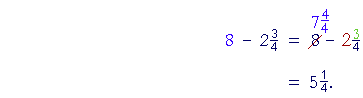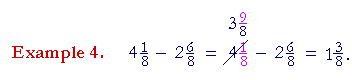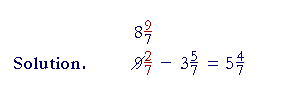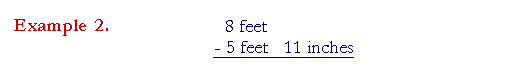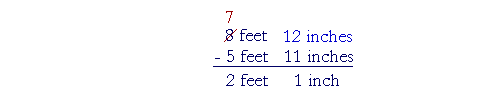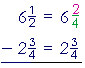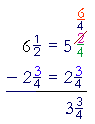S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

ADDING FRACTIONS
SUBTRACTING FRACTIONS

Lesson 24  Section 2

Regrouping

Before subtracting mixed numbers, let us subtract mixed units.

To add, subtract, or divide, the units must be the same.  We subtract hours from hours and minutes from minutes.  Now, we cannot take 40 minutes from 10 minutes.  To get more minutes, we will break off 1 of the 7 hours, and decompose it into 60 minutes.  We then regroup them with 10 minutes.

60 minutes + 10 minutes = 70 minutes:

2 hours from 6 hours are 4 hours.  40 minutes from 70 minutes are 30 minutes.

Solution.  We cannot take 11 inches from no inches, and so from 8 feet we must take 1 foot -- which is 12 inches:

5 feet from 7 feet are 2 feet.  11 inches from 12 inches are 1 inch.

We are now ready to subtract mixed numbers.  We will treat them just like mixed units.
 5.   How do we subtract a mixed number from a whole number?
  Break off 1 from the whole number and express it with the same denominator, then group the fractions.


  Example 1.      8 − 2 3
4

To subtract 3-fourths from 8, we must make fourths.  To do this,

  break off 1 from 8, and decompose it into  4
4		 :
8 = 7 + 1 = 7 4
4		 .

(Lesson 20, Example 4.)  Therefore,

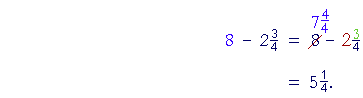
"2 from 7 is 5.    3
4		  from  4
4		  is  1
4		 ."
  Example 2. 6 − 1 2
3		   =   5 3
3		  − 1 2
3
 
    =  4 1
3		 .
  (6 = 5 3
3		 )
"1 from 5 is 4.    2
3		  from  3
3		  is  1
3		 ."

Example 3.   Subtracting mixed numbers.  Let us now compare this problem

6 1
3		  − 1 2
3
  with the previous one.  We cannot take  2
3		  from  1
3		 .  Therefore, we will again

write

6 as 5 3
3		 ,
  but here we will add the  3
3		  to  1
3		 :
6 1
3		   =   5 3
3		  +  1
3
 
    =   5 4
3		 .

Therefore,

  6 1
3		  − 1 2
3		   =  5 4
3		  − 1 2
3		   =  4 2
3		 .
"1 from 5 is 4.   2
3		  from  4
3		  are  2
3		 ."

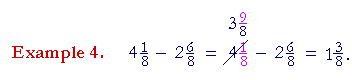
  Break off 1 from 4.  Express it as  8
8		 , and add it to  1
8		 :
4 1
8		   =  3 8
8		  +  1
8		   =  3 9
8		 .

Now the mystery if any is, How does that numerator get to be 9?

9 is the sum of the original numerator 1 and denominator 8:

1/8 + 8/8 = 9/8
  Example 5.   Write the missing numerator:  9 2
5		   = 8 ?
5
  Answer.   8 7
5

7 is the sum of denominator plus numerator:  5 + 2.

  Example 6.      9 2
7		  − 3 5
7		   = ?
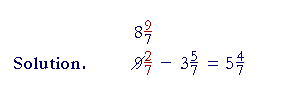
9 2
7		  becomes 8 9
7		 .  The improper numerator 9 is the sum of the
  denominator and numerator of   2
7		 :   7 + 2 = 9.

Solution.  First, we must make the denominators the same:

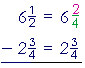
We cannot take  3
4		  from  2
4		 ; therefore, on breaking off 1 from 6, the
  fraction  2
4		  becomes 4-fourths + 2 -fourths = 6-fourths:

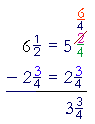
" 3
4		  from  6
4		  is  3
4		 .   2 from 5 is 3."


Please "turn" the page and do some Problems.

or

Continue on to the next Lesson.

Previous Section


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com