Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

First Principles
Here are the first principles of plane geometry -- the Definitions, Postulates, and Axioms or Common Notions -- followed by a brief commentary.
Definitions

11. An angle is the inclination to one another of two straight lines that meet.
12. The point at which two lines meet is called the vertex of the angle.

13. If a straight line that stands on another straight line makes the adjacent angles equal, then each of those angles is called a right angle; and the straight line that stands on the other is called a perpendicular to it.

14. An acute angle is less than a right angle. An obtuse angle is greater than a right angle.

15. Angles are complementary (or complements of one another) if, together, they equal a right angle. Angles are supplementary (or supplements of one another) if together they equal two right angles.

16. Rectilinear figures are figures bounded by straight lines. A triangle is bounded by three straight lines, a quadrilateral by four, and a polygon by more than four straight lines.
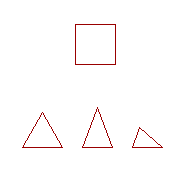
17. A square is a quadrilateral in which all the sides are equal, and all the angles are right angles.
18. An equilateral triangle has three equal sides. An isosceles triangle has two equal sides. A scalene (or oblique) triangle has three unequal sides.

19. The vertex angle of a triangle is the angle opposite the base.
10. The height of a triangle is the straight line drawn from the vertex perpendicular to the base.
11. A right triangle is a triangle that has a right angle.

12. Figures are congruent when, if one of them were placed on the other, they would exactly coincide. (Congruent figures are thus equal to one another in all respects.)

13. Parallel lines are straight lines that are in the same plane and do not meet, no matter how far extended in either direction.
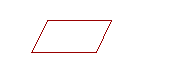
14. A parallelogram is a quadrilateral whose opposite sides are parallel
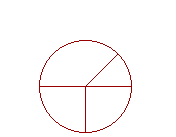
15. A circle is a plane figure bounded by one line, called the circumference, such that all straight lines drawn from a certain point within the figure to the circumference, are equal to one another.
16. And that point is called the center of the circle.
17. A diameter of a circle is a straight line through the center and terminating in both directions on the circumference. A straight line from the center to the circumference is called a radius; plural, radii.
Postulates
1. Grant the following:
1. To draw a straight line from any point to any point.
2. To extend a straight line for as far as we please in a straight line.
3. To draw a circle whose center is the extremity of any straight line, and whose radius is the straight line itself.
4. All right angles are equal to one another.
5. If a straight line that meets two straight lines makes the interior angles on the same side less than two right angles, then those two straight lines if extended, will meet on that same side.
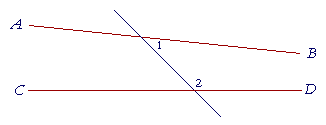
(That is, if angles 1 and 2 together are less than two right angles, then the straight lines AB, CD if extended, will meet on that same side; which is to say, AB, CD are not parallel.)
Axioms or Common Notions
1. Things that are equal to the same thing are equal to one another.

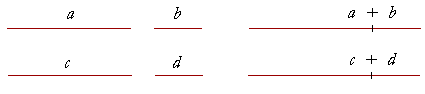
2. If equals are added to equals, the wholes (the "sums") will be
2. equal.
3. If equals are subtracted from equals, what remains will be equal.
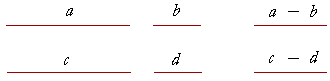
4. Things that coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Equal magnitudes have equal parts; equal halves, equal thirds,
2. and so on.
![]()
Commentary on the Definitions
A definition regulates how a word will be used. Therefore it is never a question of whether a definition is true or false. A definition is required only to be understood.
In a very significant sense, we do not need definitions. Because rather than call a figure a "triangle," we could just as well call it "a figure bounded by three straight lines." The definition eliminates the wordiness.
Definitions find their greatest importance in proofs. Because in order to prove that a triangle is equilateral, for example, we must prove that the figure satisfies the definition of "equilateral."
We say that definitions are reversible. This means that a definition is equivalent to an if and only if sentence. For example, if a triangle is equilateral, then all its sides are equal. And conversely, if all the sides of a triangle are equal, then it is called equilateral.
Note that the definition of a right angle says nothing about measurement, about 90°. Plane geometry is not the study of how to apply arithmetic to figures. In geometry we are concerned only with what we can see and reason directly, not through computation. A most basic form of knowledge is that two magnitudes are simply equal -- not that they are both 90° or 9 meters.
How can we know when things are equal? That is one of the main questions of geometry. The definition of a circle provides our first way of knowing that two straight lines could be equal. Because if we know that a figure is a circle, then we would know that any two radii are equal. (Definitions 15 and 17.)
We have chosen not to define a "point," although Euclid does. ("A point is that which has no part, that is, no magnitude or size.") And we have not defined a "line," although again Euclid does. ("A line is length without breadth.") Since there is never occasion to prove that something is a point or a line, a definition of one is not logically required. Nevertheless, with regard to a point, it is important to understand that it is the idea of position only. "Here![]() " To suppose that lines are composed of points, is a serious misunderstanding.
" To suppose that lines are composed of points, is a serious misunderstanding.
Commentary on the Postulates
The figures of geometry -- the triangles, squares, circles -- exist primarily in our inner, mental space. They are ideas. We give them incarnation by being able to draw them on paper. The fact that we can draw a figure qualifies as what we call its mathematical existence. For we may not simply assume that what we have defined, such as a "triangle" or a "circle," physically exists.
The first three Postulates narrowly set down what we are permitted to draw. Everything else we must prove. Each of those Postulates is therefore a "problem" -- a construction -- that can be accomplished.
The instruments of construction are straightedge and compass only. Postulate 1 grants that whatever we draw with a straightedge is a straight line. Postulate 3 grants that the figure we draw with a compass is a circle.
As for Postulate 5, we will have more to say about it when we come to Proposition 29.
Note, finally, that the word all, as in "all right angles" or "all straight lines," refer to all that exist, that is, that have actually been drawn. Geometry -- at any rate Euclid's -- is never just in our mind.
Commentary on the Axioms or Common Notions
The distinction between a postulate and an axiom is that a postulate is about the specific subject at hand, in this case, geometry; while an axiom is more generally true; it is in fact a common notion. Yet each has the same logical function, which is to authorize the proofs that follow.
Each of the Axioms, as well as Postulate 4, gives a criterion for things being equal (or, Axiom 5, unequal).
Implicit in these Axioms is our very understanding of equal versus unequal, which is: Two magnitudes of the same kind are either equal or one of them is greater.
So, these Axioms, together with the Definitions and Postulates, are the first principles from which our theory of figures will be deduced.
Please "turn" the page and do some Problems.
or
Continue on to Proposition 1.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2006-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com