Knowledge of figures

Geometry, which literally means land measurement, is the study of

figures.  A circle is a figure, a triangle is a figure.  What we aspire to is knowledge of figures.

A figure is whatever has a boundary.  In plane geometry, we study figures that are flat, and their boundaries are called lines, or, in the case of a circle, a single line. A line, which may be either straight or curved, is the magnitude length.  We do not mean length as opposed to width; we mean any boundary of a plane figure.

A line, too, may have its boundaries, or extremities, and we call these points.  A point is the idea of position only:  Here!  We name a line by naming its extremities with capital letters, thus we speak of the line AB.

Or we could call it BA, it does not matter, except if we want to emphasize that it extends in one direction, we would call it AB; if in the other direction, BA.

The space enclosed by the boundary -- the figure itself -- is the

magnitude area.

Magnitudes

A magnitude is whatever has size.  In plane geometry we study three kinds of magnitudes:  length, area, and angle. We compare magnitudes of the same kind -- two lengths, two areas, or two angles -- and we try to decide how they are related.  Either two magnitudes of the same kind will be equal to one another, or one of them will be larger.

Therefore if we say that these two triangles are equal --

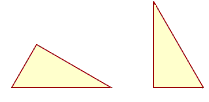
-- we mean that they are equal areas.  Because that is what kind of magnitude a triangle is.  The space enclosed by each boundary will be exactly the same.

Straight lines

Each straight line that forms the boundary of a square, for example, will have two extremities; obviously.  But we imagine that a straight line could be extended for as far as we please, and here we touch on the question of infinity. Which is something more than "for as far as we please."  It is the idea of something with no endpoints at all.

For as long as there have been mathematicians, there have been quarrels about "infinity."  What does it mean to say that something is infinite?  Not that it could be, or that it will be, but that it is.  Does what can never be whole exist?

Fortunately, for our purposes it will not be necessary to confront this knotty issue, because we will never have need of infinite lines.  It is only finite lines -- the actual or potential boundaries of a figure -- that we ever require.  Hence, when we speak of a "straight line," we will mean what people normally mean, namely a line with two extremities.

Those who think they need infinite lines imagine that any finite line, such as each side of a triangle, is but a portion
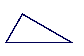of an actually infinite line. (Strange. No?)
Hence they call a finite line a "line segment." Our idea is quite the reverse, namely that we can extend any straight line for as far as we please. Such a line will be potentially infinite, but it is not actually infinite.

These quarrels about actual versus potential infinities arise only when straight lines are abstracted from the boundaries of figures. But in plane geometry it is the figures that concern us, and in the ultimate theorems, straight lines appear only as the boundaries of figures.

Also, just because we can define something (such as an actually infinite line) does not guarantee that what we have defined exists. (We can define a unicorn. But does a unicorn exist?) As we shall see, the mathematical existence of a geometrical object, as well as our ability to say that we know it, requires that we be able to draw it.

This completes the preliminary description, this is what plane geometry is about; we are now ready to study it as a logical science.

Logic

The method of logic is to know through reasoning, and it provides one answer to the question, "How do I know?"  One can reply, "I deduced it." (Latin de, away from + ducere, to lead.)  Hence when we deduce or prove something, we are led through reasoning from what we know to what we can conclude.

Just as it is not possible, however, to define every word -- we must already understand the words in which a definition is framed -- so it is not possible to prove every statement.  To prove or explain anything is to do so in terms of something else, something that we already know and accept, something more fundamental.  Logic depends, then, on what are called first principles.  These will provide the basis for proof.  The first principles of Euclid's geometry are in three categories:

1) Definitions

2) Postulates

3) Axioms or Common Notions