3
CONTINUOUS FUNCTIONS
The definition of "continuous at a point"
A theorem about continuous functions
CALCULUS BEGAN, as we noted in Lesson 1, as the study of continuous motion in a straight line.

Let the values of the variable x be the distance of a point P from the origin O, and imagine it moving from point A to point B, whose coordinates are a and b. When we say that x varies continuously in that interval, we mean: As x increases from the value a to the value b, it assumes all values between them. In other words, in going from A to B, P doesn't hop!
The values of x -- those distances from O -- constitute a continuum.
A continuous function
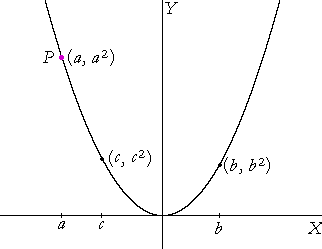
This is the graph of y = x². For every value of x, there is a value of y. And as x varies continuously from a to b, then y will vary continuously from y = a² to y = b². That is, the point P will move continuously along the graph -- from P(a, a²) to (b, b²) -- without a break.
Therefore, we say,
"The function y = x² is continuous in the interval from x = a to x = b."
But that function will be continuous in any interval on the x-axis. Therefore we say, "y = x² is a continuous function."
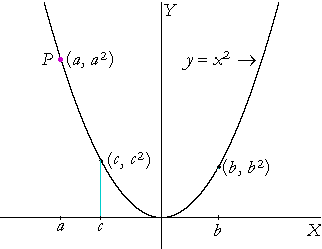
This implies the following: If x approaches c as a limit (Lesson 2), then the point P will approach (c, c²). That is, the continuous function y = x² will approach its value, c², as a limit.
We can therefore offer the following as a definition of a function being continuous at a point.
DEFINITION 3.1. Continuous at a point.
We say that a function f(x) that is defined at a point x = c
is continuous at that point
if and only if
as x approaches c as a limit,
f(x) approaches f(c) as a limit. (Definition 2.1.)
In symbols:
if and only
if f(x) is continuous at x = c. If a function is continuous at every point in an interval, then we say that the function is continuous in that interval. And if a function is continuous in any interval, then we simply call it a continuous function. Calculus is fundamentally about functions that are continuous at every point in their domains. Prime examples of continuous functions are polynomials (Lesson 2).
Problem 1. a) Prove that this polynomial, 2x² − 3x + 5, a) is continuous at x = 1. To see the answer, pass your mouse over the colored area.
We must apply the definition of continuous at a point, Definition 3.1. That is, we must show that when x approaches 1 as a limit, f(x) approaches f(1), which is 4. b) Can you think of any value of x where that polynomial -- or any
You should not be able to. Polynomials are continuous everywhere. As x approaches any limit c, any polynomial In addition to polynomials, the following functions also are continuous at every point in their domains. Rational functions Root functions Trigonometric functions Inverse trigonometric functions Logarithmic functions Exponential functions These are the functions that one encounters throughout calculus. To evaluate the limit of any one of these as x approaches a value, simply evaluate the function at that value.
![]()
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
And according to the Theorems of Lesson 2, that is true.
f(x) therefore is continuous at x = 1.
b) polynomial -- would not be continuous?
P(x) approaches P(c). (Lesson 2)
| Example 1. Evaluate |
| Solution. |
The student should have a firm grasp of the basic values of the trigonometric functions. In calculus, they are indispensable. See Topics 16 and 17 of Trigonometry.
| Problem 2. Evaluate |
sin 0 = 0
| Problem 3. Evaluate |
![]()
| * | * | * |
Here, by contrast, is the graph of a function that has a point of discontinuity.

| This is the graph of y = | 1 x |
. At x = 0, the function is not defined, |
because division by 0 is an excluded operation. (Skill in Algebra, Lesson 6.) x = 0 is a point of discontinuity. In fact, as x approaches 0 -- whether from the right or from the left -- y does not approach any number![]()
Nevertheless, as x increases continuously in an interval that does not include 0, then y will decrease continuously in that interval. We say,
| "The function y = | 1 x |
is continuous for all values of x except x = 0." |
In the applications of calculus, functions will be continuous in certain intervals. And as we saw in Problem 1, to evaluate a limit there, simply evaluate the function at that point.
![]()
Example 2. Consider this function:
| f(x) | = | x² − 4 x − 2 |
This function is undefined at x = 2, and therefore it is discontinuous there; however, we will return to this point below.
The function nevertheless is defined at all other values of x, and it is continuous at all other values.
For example, as x approaches 8, then according to the Theorems of Lesson 2, f(x) approaches f(8).
| f(8) = | 60 6 |
= 10. |
f(x) therefore is continuous at x = 8. (Definition 3.1.)
In this same way, we could show that the function is continuous at all values of x except x = 2.
A removable discontinuity
For a function to be continuous at x = c, it must exist at x = c. However, when a function does not exist at x = c, it is sometimes possible to assign a value to the function so that it will be continuous there.
This function
| f(x) | = | x² − 4 x − 2 |
does not exist at x = 2. But for every value of x![]() 2:
2:
| x² − 4 x − 2 |
= | (x + 2)(x − 2) x − 2 |
= | x + 2. |

Therefore, as x approaches 2,
![]()
(Compare Example 2 of Lesson 2.) That is,
![]()
Now, f(x) is not defined at x = 2 -- but we could define it. We could define it to have the value of that limit![]() We could say,
We could say,
"At x = 2, let f(x) have the value 4."
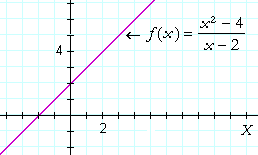
If we do that, then f(x) will be continuous at x = 2 -- because the limit at that point will be the value at that point.
![]()
When we are able to do that -- define a function at a point where it is undefined and therefore discontinuous -- we say that the function has a removable discontinuity.
f(x) above is such a function.
Problem 2. Consider this function:
| y = | 5x x |
. |
a) For which value of x is this function discontinuous? x = 0.
b) Define the function there so that it will be continuous.
For all values except x = 0, the function has the value 5. Hence, if we define the function to have the value 5 at x = 0, then we have successfully removed the discontinuity.
A theorem about continuous functions
Let f(x) = 5x and g(x) = x3. And let us consider
![]()
Since f is continuous, then the limit as x approaches 2 will be the value
f (g(2)).
![]()
(See Topic 3 of Precalculus.)
Now let us consider
![]()
That is, let us first take the limit of g. But since g is continuous, that limit will be g(2). We will have
![]()
In other words:
![]()
Next Lesson: The "limit" infinity (∞)
www.proyectosalonhogar.com
