4
THE "LIMIT" INFINITY (∞)
The definition of "becomes infinite"
INFINITY, the student will see, is not a number, it is not a place -- and it is not a limit. Like any defined word, "infinity" stands for an idea that requires many words. In fact, when we say that the limit of a variable "becomes infinite" -- we mean that it does not approach a limit![]()
DEFINITION 4.1. "becomes infinite." If the absolute values of a variable (x or y) become and remain greater than any positive number we might name, however large, then we say that the variable "becomes infinite."
| Consider again | y | = | 1 x |
. |

If x becomes a very small number -- if it approaches 0 from the
| right, say -- then y, its reciprocal, | , becomes a very large number. | 1 x |
will become and remain greater, for example, than 10100000000. y becomes infinite.
We write, in this case,
![]()
Now, although we write "lim," we do not mean it -- because no limit
| exists. When x approaches 0, | 1 x |
does not approach any number, and a |
limit is a number. We write "lim = ∞" as shorthand for saying that there is no limit; the function becomes larger than any number we might name.
| If x approaches 0 from the left, then | 1 x |
becomes a large negative |
number. We write
![]()
When a function becomes infinite in this way as x approaches a value, that indicates the function is discontinuous at that value. (Definition 3.1.)
| Hence the function y = | 1 x |
is discontinuous at x = 0. |
Whenever a function becomes infinite as x approaches a value a, then the line x = a is a vertical asymptote of the graph. (Topic 18 of
| Precalculus.) The graph of y = | 1 x |
, then, has a vertical asymptote at x = 0. |
Next, let us consider the case when x becomes infinite, that is, when it becomes a large positive number -- when it takes on values to the extreme right of 0.

| Then | 1 x |
does approach a limit. It becomes a very small number, |
namely 0. We write
![]()
(We should speak in this case of the "limit as x becomes infinite," not as x "approaches infinity." Because again, infinity is neither a number nor a place.)
Finally, when x becomes infinite negatively, that is, when it assumes
| values to the extreme left of 0 (−∞), then again | 1 x |
approaches 0. We |
write
![]()
| In other words, whenever x approaches ±∞, the values of y = | 1 x |
approach the horizontal line y = 0. That horizontal line is called a horizontal asymptote of the graph.
| Problem 1. Evaluate |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
![]()
| tan x does not exist at | π 2 |
. There is no limit. (Topic 17 and |
| Topic 19 of Trigonometry.) As x approaches | π 2 |
from the right, tan x |
becomes larger than any number we might name. (Definition 4.1.)
Limits of rational functions
A rational function is a quotient of polynomials (Topic 6 of Precalculus). It will have the form
| f (x) g (x) |
where f and g are polynomials (g ![]() 0).
0).
Apart from the constant term, each term of a polynomial will have a factor xn (![]() ). Therefore let us investigate the following limits. c could be any constant except 0.
). Therefore let us investigate the following limits. c could be any constant except 0.
The student should complete each right-hand side as a problem.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do it yourself first!
| 1) | = | 0 | |
| 2) | = | ∞ | |
| 3) | = | ∞ | |
| 4) | 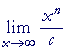 |
= | ∞ |
| Example. Prove: | 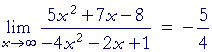 |
Solution. Divide the numerator and denominator by the highest power of x. In this case, divide them by x²:
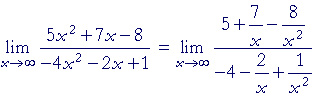
According to 1), above, the limit of each term that contains x is 0. Therefore by the theorems of Topic 2, we have the required answer.
In similar cases, the first step is: Divide the numerator and denominator by the highest power of x present in either.
| Problem 2. | = | 4 |
On dividing both numerator and denominator by x, the result follows.
| Problem 3. | 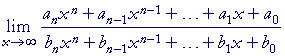 |
= |
In other words: When the numerator and denominator are of equal degree,
then the limit as x becomes infinite is equal to the quotient of the leading coefficients.
Problem 4.
| |
= | 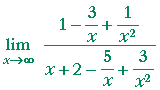 |
= | = | 0 |
| |
= | = | ∞ |
This problem illustrates:
When the degree of the denominator is greater than the degree of the numerator -- that is, when the denominator dominates -- then the limit as x becomes infinite is 0. But when the numerator dominates -- when the degree of the numerator is greater -- then the limit as x becomes infinite is ![]() .
.
Change of variable
Consider this limit:
![]()
Rather than have the variable approach 0, we sometimes prefer that it become infinite. In that case, we do a change of variable. We put
| x | = | 1 z |
| or | 1 n |
or | 1 t |
, it does not matter. For, x approaching 0 is equivalent to |
z becoming infinite. Then
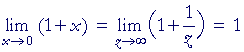
| On replacing x with | 1 z |
, we let z become infinite. The limit remains 1. |
Where will this come up? In the limit from which we calculate the number e :
![]()
(Lesson 15.)
Problem 5. In the above limit, change the variable to n, and let it become infinite.
![]()
![]()
www.proyectosalonhogar.com
