The derivative. Lesson 5, Section 2: Problems
The derivative of f(x) = 2x − 5
Problem 1. Let f(x) = 2x − 5.
a) Write the difference quotient and simplify it.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| f(x + h) − f(x) h |
= | 2(x + h) − 5 − (2x − 5) h |
| = | 2x + 2h − 5 − 2x + 5 h |
|
| = | 2h h |
|
| = | 2. | |
b) Evaluate f '(x).
| f '(x) | = | 2 | |
| = | 2, | ||
according to Theorem 4 of Lesson 2.
So, the slope of the tangent line to this curve is everywhere equal to 2. But that is obvious. f(x) = 2x − 5 is itself a straight line whose slope is 2! (Topic 9 of Precalculus.)
Problem 2.
a) Calculate the derivative of f(x) = x3. Follow the sequence of
a) Problem 1.
a) [Hint: (a + b)3 = a3+ 3a²b + 3ab² + b3. Topic 24 of Precalculus.]
| f(x + h) − f(x) h |
= | (x + h)³ − x³ h |
|
| = | x³ + 3x²h + 3xh² + h³ − x³ h |
||
| = | 3x²h + 3xh² + h³ h |
||
| = | 3x² + 3xh + h². | ||
| f '(x) | = | (3x² + 3xh + h²) | |
| = | 3x². | ||
b) Evaluate the slope of the tangent to y = x3 at x = 4.
The slope at x is 3x². Therefore, at x = 4, the slope is 3· 16 = 48.
c) Evaluate the slope of the tangent to y = x3 at x = −2.
3· (−2)² = 3· 4 = 12
d) What is the rate of change of f(x) = x3 at x = −1.
3· (−1)² = 3· 1 = 3
At x = −1, the function is increasing at the rate of 3 units of y per unit of x.
e) What is the rate of change of that function at x = 5.
3· 5² = 3· 25 = 75
At x = 5, the function is increasing at the rate of 75 units of y per unit of x.
Problem 3.
| a) Show: | d dx |
1 x |
= − | 1 x² |
. |
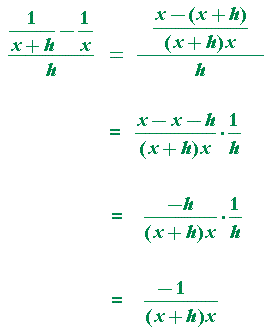
| d dx |
1 x |
= | ||
| = | ||||
To see how the difference quotient was simplified, see Lesson 3 of Precalculus, Problem 10c.
b) What is the rate of change of the function at x = 4?
| At x = 4, − |
1 x² |
= − |
1 16 |
. The function is decreasing at the rate |
| of |
1 16 |
of a unit of y per unit of x. |
c) What is the rate of change of the function at x = ¼?
| At x = ¼, − |
1 x² |
= −16. The function is decreasing at the |
rate of 16 units of y per unit of x.
Look at the graph. The closer to 0, the greater the rate of change. The further away from 0, the smaller the rate of change.
At every point of that graph, the tangent has a negative slope -- the derivative is always negative. As we move from left to right, the values of that function always decrease.
We have the following result, then:
| d dy |
1 x |
= − | 1 x² |
. |
That is,
| d dy |
x−1 = −x−2. |
This has the form
| d dy |
xn = nxn−1 |
In what follows we will be exploiting that form.
![]()
Next Lesson: Rules for derivatives
www.proyectosalonhogar.com