9
INSTANTANEOUS VELOCITY
AND
RELATED RATES
ONE OF THE most important applications of calculus is to motion in a straight line, which is called rectilinear motion.
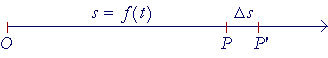
Consider a point P moving in a straight line. Let s be the distance (or space) measured from a fixed point O to any position of P, and let t be the time elapsed. Then to each value of t there will correspond a distance s. s will be a function of t:
s = f(t).
When we know f(t), we have what is called the equation of motion.
Now, in a time interval Δt, there will be a change Δs -- P will move to the point P'. By definition,
| Δs Δt |
= | The average velocity in moving from P to P'. |
For example, if at t = 30 sec, s = 100 meters,
and at t = 35 sec, s = 210 m, then
| Δs Δt |
= | 110 m 5 sec |
= | 22 meters per second. |
But that is the average velocity in moving between those two points. The question calculus asks is: What is the exact velocity at the point P itself?

If P moves with constant velocity -- which is called uniform motion -- then we don't need calculus for that. In other words, if the equation of motion is
s = 22 t,
then at every instant of time, the velocity is 22 m/sec. For, the slope of that line, which is 22, is rate of change of s with respect to t, which by definition is the velocity.
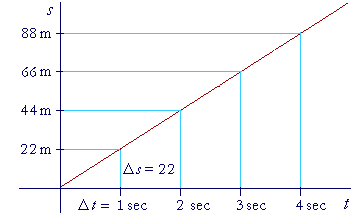
In each 1 second of time, the point P moves a distance of 22 meters.
| Δs Δt |
= | 22 meters per second. |
That is not a realistic pitcture, of course, because at 0 seconds the velocity is surely not 22 meters/sec![]() There must have been an acceleration
There must have been an acceleration
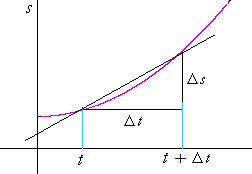
to that constant velocity. During that acceleraltion, the velocity was not uniform. The graph was not a straight line.
For any kind of motion, then, uniform or not, we define the instantaneous velocity at the time t to be the limit of the average velocity, Δs/Δt, as Δt approaches 0.
| v(t) | = | ds dt |
"The velocity at any instant t
is the derivative of the distance with respect to the time
evaluated at time t."
Compare Lesson 5.
Example. Let the following be the equation of motion:
s(t) = 6t ² + t + 8
Let t be measured in seconds and s in meters.
a) What is the position -- the distance from the origin -- at the end of 10 seconds?
Answer. s(10) = 6· 10² + 10 + 8 = 618 meters.
b) What is the velocity at the end of 10 seconds?
| Answer. | ds dt |
= | 12t + 1 |
| = | 12· 10 + 1 | ||
| = | 121 m/sec. | ||
Problem 1. It has been found by experiment that a body falling from rest under the influence of gravity, follows approximately this equation of motion:
s(t) = 9.8 t ².
s is the distance fallen measured in meters; t is the time elapsed measured in seconds.
a) At the end of 3 seconds, how far has the body fallen?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
s(3) = 9.8 × 3² = 9.8 × 9 = 88.2 m.
a) What is its velocity at the end of 3 seconds?
| ds dt |
= | 19.6 t |
| = | 19.6 × 3 | |
| = | 58.8 m/sec. | |
The second derivative
The derivative of y = f(x) -- y'(x) -- will itself be a function of x. This new function may also be differentiable, in which case we call the derivative of the first derivative of y the second derivative. The notation for
| the second derivative is | or y''. |
Consider this equation of motion,
s(t) = 3t ².
Then the first derivative is the velocity v:
| v = | ds dt |
= 6t. |
The second derivative is the rate of change of the velocity with respect to time. That is called the acceleration a:
| a = | d²s dt² |
= 6. |
If t is measured in seconds and s in meters, then the units of velocity are meters per second, which we abbreviate as m/sec. The units of acceleration are then meters per second per second, which we abbreviate as m/sec².
Problem 2. A body moves in a straight line according to this equation of motion:
s(t) = 10t ² − 4t + 8,
where t is measured in seconds and s in meters.
a) What is its position at the end of 5 sec?
s(5) = 10· 5² − 4· 5 + 8 = 238 m.
b) What is the equation for its velocity v at any time t ?
| v(t) = | ds dt |
= 20t − 4. |
c) What is its velocity v at at the end of 5 seconds?
v(5) = 20· 5 − 4 = 96 m/sec.
d) What is the equation for its acceleration a at any time t ?
| a(t) = | d²s dt² |
= | dv dt |
= 20. |
e) What is its acceleration at the end of 5 seconds?
a(5) = 20 m/sec².
Problem 3. Under the influence of gravity, a body moves according to this equation of motion:
s(t) = ½gt ² + s0
a) What is the physical significance of the constant s0?
It is the body's initial position, s(0).
b) How fast is the body moving after 5 seconds?
| v(t) = | ds dt |
= gt. At t = 5, v(5) = 5g. |
c) What is the physical significance of the constant g?
| g = | d²s dt² |
. g is the acceleration due to gravity, which is |
approximately 9.8 m/sec².
Related rates
Example 1.
a) If the radius of a circle is expanding, write the equation that shows
a) how fast the area of the circle is expanding. (A = πr².)
| Solution. We are to calculate | dA dt |
. We have |
| A | = | πr². | ||
| On differentiating implicitly with respect to t (Lesson 8): | ||||
| dA dt |
= | = | ||
b) If the radius is expanding at the rate of 2 cm/min, how fast is the area
a) expanding when the radius is 15 cm?
| Solution. We are given that | dr dt |
= 2 cm/min. Therefore, when |
r = 15 cm,
| dA dt |
= | 2π· 15· 2 |
| 188.4 cm²/min. |
Example 2. A boy is walking at the rate of 5 miles per hour toward the foot of a flag pole 60 feet high. At what rate is he approaching the top of the pole when he is 80 feet from its foot?
Solution. Draw a picture![]() In all problems of this type, draw a picture.
In all problems of this type, draw a picture.
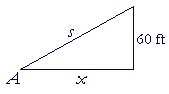
Let the boy be at the point A at a distance x from the foot of the flag pole. Let s be his distance from the top of the pole.
| We are to calculate | ds dt |
. |
The figure is a right triangle. Therefore,
| 1) | s² = x² + 3600. |
Differentiate implicitly with respect to t.
| 2s | ds dt |
= | 2x | dx dt |
. |
That is,
| ds dt |
= | x s |
dx dt |
. |
| Now, we are given x = 80 feet, and | dx dt |
= −5 mi/hour. We write the |
minus sign because x is decreasing as he approaches the flag pole.
According to line 1),
![]()
Therefore,
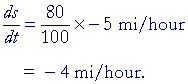
Problem 4. The side of an square is a cm long, and is increasing at the rate of b cm per hour. How fast is the area increasing?
2ab cm²/hour.
Problem 5. The side of an equilateral triangle is a cm long, and is increasing at the rate of b cm per hour. How fast is the area increasing?
½ab ![]() cm²/hour.
cm²/hour.
Problem 6.
a) The surface area S of a sphere is given by the formula S = 4πr².
If r changes with time, how does S change?
| dS dt |
= | 8πr | dr dt |
| b) The volume V of a sphere is given by the formula V = | 4 3 |
πr3. |
If r changes with time, how does V change?
| dV dt |
= | 4πr² | dr dt |
| c) Prove: | dV dt |
= | ½r | dS dt |
. |
| dV dt |
= | 4πr² | dr dt |
= ½· 8πr² | dr dt |
= ½r· 8πr | dr dt |
= ½r | dS dt |
. |
Problem 7. The base and height of a rectangle are b and h, and they are changing at the rates p, q respectively. Prove that the area A is changing at the rate bq + hp.
A = bh.
According to the product rule:
| dA dt |
= | b | dh dt |
+ | h | db dt |
= | bq + hp. |
Problem 8.
a) A ladder 50 feet long is leaning against a wall. If the foot of the ladder
a) is being pulled away from the wall at a certain rate, derive the formula
a) for how fast the top of the ladder is descending.
a) (Let x be the distance of the foot of the ladder from the wall,
a) and let h be the distance of the top from the ground. Draw a
a) picture![]() )
)
| dh dt |
= − | x h |
dx dt |
= | 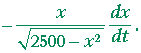 |
If the foot is being pulled away at the rate of 3 ft/min, then
b) when the foot is 14 feet from the wall, how fast is the top
b) descending?
7/8 ft/min.
c) when is the top descending at the rate of 4 ft/min?
When the bottom is 40 feet from the wall.
d) When will the top and bottom move at the same rate?
When the bottom is 25![]() feet from the wall.
feet from the wall.
![]()
Next Lesson: Maximum and minimum values
www.proyectosalonhogar.com
