8
MORE RULES
FOR
DERIVATIVES
The derivative of an inverse function
The quotient rule
The following is called the quotient rule:
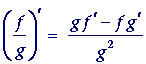
"The derivative of the quotient of two functions
is equal to
the denominator times the derivative of the numerator
minus the numerator times the derivative of the denominator
all divided by the square of the denominator."
For example, accepting for the moment that the derivative of sin x is cos x (Lesson 12):
![]()
| Problem 1. Calculate the derivative of | x² sin x |
. |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| sin x· 2x − x² cos x sin2x |
| Problem 2. Use the chain rule to calculate the derivative of | sin²x x3 |
. |
|
x³· 2 sin x cos x − sin²x· 3x² x6 |
= |
x² sin x(2x cos x − 3 sin x) x6 |
| = |
sin x(2x cos x − 3 sin x) x4 |
|
| Problem 3. Calculate the derivative of | x² − 5x − 6 2x + 1 |
. |
| (2x + 1)(2x − 5) − (x² − 5x − 6)· 2 (2x + 1)² |
= | 4x² − 8x − 5 − 2x² + 10x + 12 (2x + 1)² |
| = | 2x² + 2x + 7 (2x + 1)² |
|
| Problem 4. Calculate the derivative of | 3x² − x + 4 |
. |
See the Example, Lesson 6.
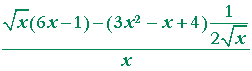 |
= | 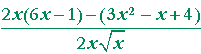 |
| = | 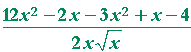 |
|
| = | ||
Proof of the quotient rule
| THEOREM. | 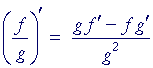 |
Proof. Since g = g(x), then
| d dx |
1 g |
= | d dg |
1 g |
· | dg dx |
= − | 1 g² |
g' |
according to the chain rule, and Problem 3 of Lesson 5.
Therefore, according to the product rule (Lesson 6),
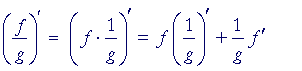
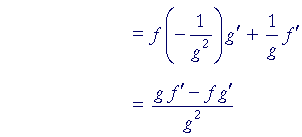
This is the quotient rule, which we wanted to prove.
Implicit differentiation
Consider the following:
x² + y² = r²
This is the equation of a circle with radius r. (Lesson 17 of Precalculus.)
| Let us calculate | dy dx |
. | To do that, we could solve for y and then take the |
derivative. But rather than do that, we will take the derivative of each term. We will assume that y is a function of x, and we will apply the
| chain rule. Then we will solve for | dy dx |
. |
| d dx |
x² | + | d dx |
y² | = | d dx |
r² |
| 2x + 2y | dy dx |
= | 0 | |||
| dy dx |
= | − | x y |
. | ||
This is called implicit differentiation. y is implicitly a function of x. The result generally contains both x and y.
Problem 1.
a) In this circle,
x² + y² = 25,
a) what is the y-coordinate when x = −3?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
y = 4 or −4. For,
(−3)² + (±4)² = 5²
b) What is the slope of the tangent to the circle at (−3, 4)?
| 3 4 |
. For, the derivative is − | x y |
. |
c) What is the slope of the tangent to the circle at (−3, −4)?
| − | 3 4 |
Problem 2. In the first quadrant, what is the slope of the tangent to this circle,
(x − 1)² + (y + 2)² = 169,
when x = 6?
[Hint: 5² + 12² = 13² is a Pythagorean triple.]
In the first quadrant, when x = 6, y = 10.
(6 − 1)² + (10 + 2)² = 13².
| y' = − | x − 1 y + 2 |
. Therefore the slope is − | 6 − 1 10 + 2 |
= − | 5 12 |
Problem 3. 15y + 5y3 + 3y5 = 15x. Calculate y'.
| 15y' + 15y²y' + 15y4y' | = | 15 |
| y'(1 + y² + y4) | = | 1 |
| y' | = |
1 1 + y² + y4 |
| Problem 4. | Calculate y'. |
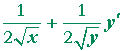 |
= | 0 |
| = | ||
| y' | = | |
Problem 5. Calculate the slope of the tangent to this curve at (2, −1):
x3 − 3xy² + y3 = 1
| 3x² − (3x· 2y y' + y²· 3) + 3y² y' | = | 0 | ||
| according to the product rule. | ||||
| 3x² − 6xy y' − 3y² + 3y² y' | = | 0 | ||
| x² − 2xy y' − y² + y² y' | = | 0 | ||
| y'(y² − 2xy) | = | y² − x² | ||
| y' | = | y² − x² y² − 2xy |
||
| Therefore, at (2, −1): | ||||
| y' | = | (−1)² − 2² (−1)² − 2· 2· −1 |
||
| = | −3 5 |
|||
| = | − | 3 5 |
||
The derivative of an inverse function
When we have a function y = f(x) -- for example
y = x²
-- then we can often solve for x. In this case,
![]()
On exchanging the variables, we have
![]()
| is called the inverse function of y = x². |
Let us write
| f(x) | = | x² |
| g(x) | = | |
And let us call f the direct function and g the inverse function. The formal relationship between f and g is the following:
f( g(x)) = g( f(x)) = x.
(Topic 19 of Precalculus.)
Here are other pairs of direct and inverse functions:
| f(x) | = | sin x | g(x) | = | arcsin x | |
| f(x) | = | ax | g(x) | = | logax | |
| f(x) | = | x3 | g(x) | = | ||
Now, when we know the derivative of the direct function f, then from it we can determine the derivative of g.
Thus, let g(x) be the inverse of f(x). Then
f(g(x) = x.
Now take the derivative with respect to x:
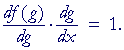
This implies:
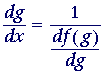
"The derivative of an inverse function is equal to
the reciprocal of the derivative of the direct function
when it is expressed as a function of the inverse function."
| Example. Let f(x) = x², and | Then f( g) = g². |
Therefore,
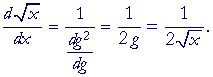
![]()
Next Lesson: Velocity and rates of change
www.proyectosalonhogar.com
