THE LINE VALUE of a trigonometric function is a straight line whose length represents the value of the function.  For as the central angle changes, the line value becomes a kind of "graph" of the function during one revolution.  It is the best way for the student to visualize and remember each function's values, in particular those of the sine, cosine, and tangent.

The line values

The line values of the functions of angle θ are now as follows; to avoid scrolling, the figure below is the same:

A complete cycle of sin θ

The student with a good imagination should now try to follow the point B as it makes a complete circuit about the unit circle.  In particular, let us visualize what happens to CB, the line value of sin θ.

At θ = 0°, the point B coincides with D, so that CB vanishes.  sin 0° = 0.

As θ increases in the first quadrant, CB also increases until it reaches its maximum value at 90°.   CB coincides there with the unit radius AF, so that CB = AF = sin 90° = 1.

When θ enters the second quadrant, CB begins to decrease in value.  At 180°, B coincides with K, and CB vanishes again.  sin 180° = 0.

In the third quadrant, CB increases in absolute value, but the sine in that quadrant is negative.  At 270°, CB coincides with AL.   sin 270° has its algebraic minimum:  sin 270° = −1.

Finally, in the fourth quadrant, CB decreases in absolute value until B coincides once again with D.  sin 360° = sin 0° = 0.

We see that sin θ never has a value greater than 1 (at 90°), or less than −1 (at −90°).

−1 ≤ sin θ ≤ 1.

A complete cycle of cos θ

The line value of cos θ is AC.  As the point B revolves, C shuttles back and forth along the diameter DK.  At 0°, AC coincides with the unit radius AD, so that cos 0° = 1.

At θ = 90°, C coincides with A, so that AC vanishes.  cos 90° = 0.

At θ = 180°, C reaches K.   AC = AK = cos 180° = −1.

At θ = 270°, C is back at A.   cos 270° = 0.

Finally, at θ = 360°, AC coincides again with the radius AD.   cos 360° = 1.

cos θ (AC) also has a maximum value of 1 (at 0°), and minimum of −1 (at 180°).

−1 ≤ cos θ ≤ 1.

A complete cycle of tan θ

Finally, it will be extremely instructive to follow DE and KE, the line values of tan θ.

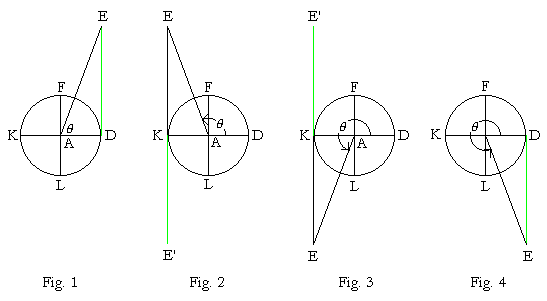
At θ = 0° (Fig. 1), the point E coincides with D, so that the tangent line DE vanishes.  tan 0° = 0.

As θ increases towards 90° (Fig. 1), DE remains tangent to the circle — its length getting longer and longer.  At 90°, DE is parallel to AF -- there is no more triangle.  tan 90° does not exist.

In the second quadrant (Fig. 2), the tangent line jumps to KE.  (We call that a discontinuity in the function.)  In the second quadrant, however, tan θ is algebraically negative, and we indicate that by the line KE'.

At θ = 180°, the line value KE is again 0.

In the third quadrant (Fig. 3), the line value is KE, but tan θ is algebraically positive (KE').  At θ = 270°, KE becomes parallel to AL, so that tan 270° does not exist.

In the fourth quadrant (Fig. 4), KE jumps over to DE (another discontinuity), and at θ = 360°, tan 360° = tan 0° = 0.

Projections

The straight line CD is called the vertical projection of the straight line AB.  (The straight lines BD, AC are drawn perpendicular to CD.  It is as if a light were shining on AB, and CD is the shadow.)

EF is called the horizontal projection of AB.

Now, if AB is a unit radius, then BC -- the line value of sin θ -- is the

vertical projection of the radius.  And AC -- the line value of cos θ -- is the horizontal projection.

Thus in a unit circle, sin θ is the vertical projection of the radius.  cos θ is the horizontal projection.