Problem 1. Which numbers are indicated by the following, where n could be any integer?
a) 2nπ
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
The even multiples of π:
0, ±2π, ±4π, ±6π, . . .
By '2n' we mean to signify an even number.
b) (2n + 1)π
The odd multiples of π:
±π, ±3π, ±5π, ±7π, . . .
By '2n + 1' we mean to signify an odd number.
Zeros
By the zeros of sin θ, we mean those values of θ for which sin θ will equal 0.
Now, where are the zeros of sin θ? That is,
sin θ = 0 when θ = ?
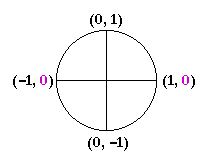
We saw in Topic 16 on the unit circle that the value of sin θ is equal to the y-coordinate. Hence, sin θ = 0 at θ = 0 and θ = π -- and at all angles coterminal with them. In other words,
sin θ = 0 when θ = nπ.
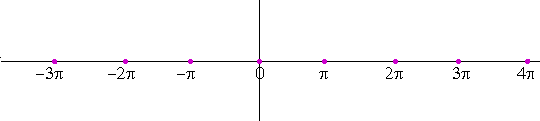
This will be true, moreover, for any argument of the sine function. For example,
sin 2x = 0 when the argument 2x = nπ;
that is, when
The period of a function
When the values of a function regularly repeat themselves, we say that the function is periodic. The values of sin θ regularly repeat themselves
every 2π units. Hence, sin θ is periodic. Its period is 2π.
Definition. If, for all numbers x, the value of a function at x + p is equal to the value at x --
If f(x + p) = f(x)
-- then we say that the function is periodic and has period p.

The function y = sin x has period 2π, because
sin (x + 2π) = sin x.
The height of the graph at x is equal to the height at x + 2π -- for all x.
Problem 3.
a) In the function y = sin x, what is its domain?
a) (See Topic 3 of Precalculus.)
x may be any real number. − < x <
< x <  .
.
b) What is the range of y = sin x?
sin x has a minimum value of −1, and a maximum of +1.
−1  y
y  1
1
For example, if a = 2 --
y = sin 2x
-- that means there are 2 periods in an interval of length 2π.
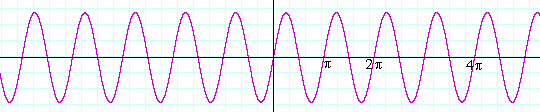
If a = 3 --
y = sin 3x
-- there are 3 periods in that interval:

While if a = ½ --
y = sin ½x
-- there is only half a period in that interval:
The constant a thus signifies how frequently the function oscillates; so many radians per unit of x.
(In physics, when the independent variable is the time t, the constant is written as ω ("omega"). sin ωt. ω is called the angular frequency; so many radians per second.)
Problem 4.
a) For which values of x are the zeros of y = sin mx?
| At mx = nπ; that is, at x =
|
nπ
m |
. |
b) What is the period of y = sin mx?
| |
2π
m |
. Since there are m periods in 2π, then one period is 2π |
divided by m. Compare the graphs above.
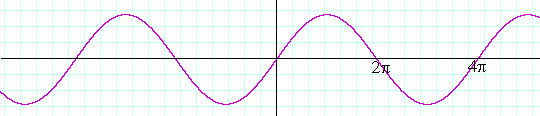
Problem 5. y = sin 2x.
a) What does the 2 indicate?
In an interval of length 2π, there are 2 periods.
b) What is the period of that function?
c) Where are its zeros?
Problem 6. y = sin 6x.
a) What does the 6 indicate?
In an interval of length 2π, there are 6 periods.
b) What is the period of that function?
c) Where are its zeros?
Problem 7. y = sin ¼x.
a) What does ¼ indicate?
In an interval of length 2π, there one fourth of a period.
b) What is the period of that function?
2π/¼ = 2π· 4 = 8π
c) Where are its zeros?
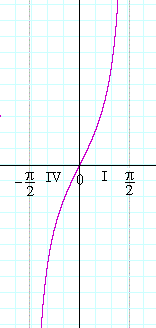
Precalculus.)
Now in the 2nd Quadrant (Fig. 2), the graph has exactly the same negative values (KE') as in the 4th (DE).
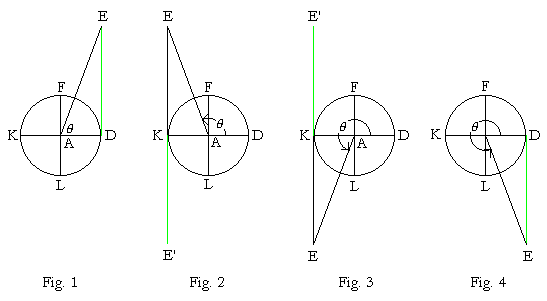
And in the 3rd Quadrant (Fig. 3), the graph has exactly the same positive values (KE') as in the 1st (DE).
Thus the graph of Quadrants IV and I is repeated in Quadrants II and III, and periodically along the entire x-axis.
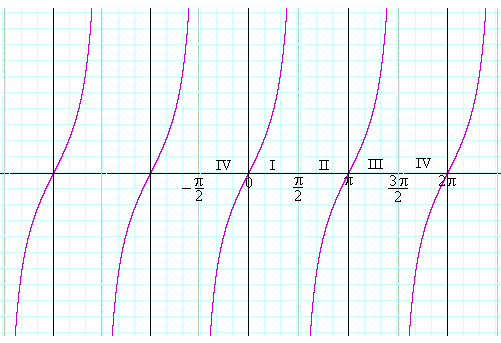
This is the graph of y = tan x.
Next Topic: Inverse trigonometric functions
The Topics | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com