14 RADIAN MEASURE IN THE RADIAN SYSTEM of angular measurement, the measure of one revolution is 2π. (In the next Topic, Arc Length, we will see the actual definition of radian measure.) 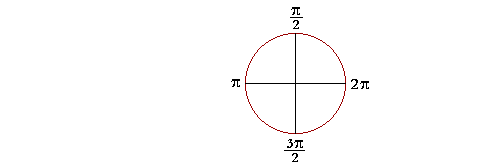
Half a circle, then, is π. And, most important, each right angle is half
Radians into degrees The student should have a clear picture of the following: 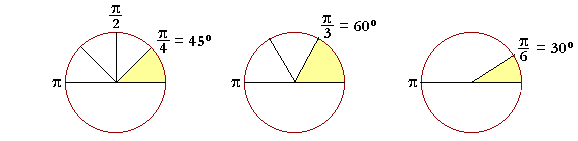
Arithmetic, Multiplying and dividing fractions, Question 5.)
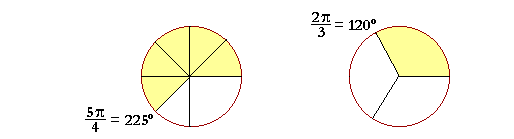
Problem 1. Convert each of these radian measures into degrees. Problem 1. The student should know these. To see the answer, pass your mouse over the colored area.
Problem 2. Convert each of these radian measures into degrees.
Problem 3. Evaluate the following. (See Topic 6 and Topic 7.)
Problem 4. In terms of radians, what angle is the complement of an
Problem 5. A function of any angle is equal to the cofunction of its complement. (Topic 5.) Therefore, in terms of cofunctions:
Degrees into radians 360° = 2π. 180° = π. When we write, 180° = π, we mean that it equals π radians, which is approximately 3.14 radians. However, we normally omit the word radians. For, as we will see in the next Topic, Arc length, the radian measure can be any number. Example 1. Convert 120° into radians. Solution. We can go from what we know to what we don't know. Since
Or, since 120° is a third of 360°, which is 2π, then
In general, proportionally,
so that
Example 3. Change 140° to radians.
upon dividing both the numerator and denominator first by 10 and then by 2. (Lesson 21 of Arithmetic, and Lesson 1.) Problem 6. Change each of the following into radians.
Coterminal angles Angles are coterminal if they have the same terminal side. 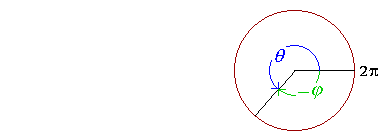
θ is coterminal with −φ. They have the same terminal side. Notice that θ + φ = 2π, so that θ = 2π − φ . . . . . . . . (1) Example 4. Name in radians the non-negative angle that is coterminal
Answer. Let us call that angle θ. Then according to line (1),
See Lesson 23 of Algebra, Example 7. Problem 7. Name in radians the non-negative angle that is coterminal with each of the following, and is less than 2π.
The multiples of π Starting at 0, let us go around the circle a half-circle at a time. We will then have the following sequence, which are the multiples of π: 0, π, 2π, 3π, 4π, 5π, etc. 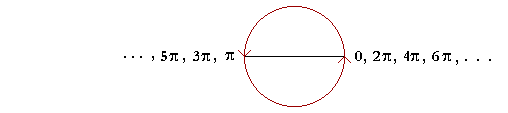
The point to see is that the odd multiples of π, π, 3π, 5π, 7π, etc. are coterminal with π. While the even multiples of π, 2π, 4π, 6π, etc. are coterminal with 0. If we go around in the negative direction, 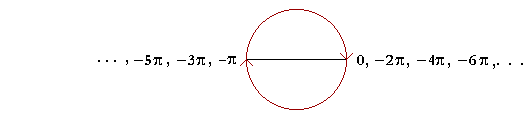
we can make a similar observation. Problem 8. Name in radians the non-negative angle that is coterminal with each of the following, and is less than 2π. a) -π π b) -2π 0 c) -3π π d) -4π 0 e) -5π π f) 3π π g) 4π 0 h) 5π π i) 6π 0 j) 7π π www.proyectosalonhogar.com |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||