Triángulo:
Es un poligono que tiene tres lados y tres ángulos.
El punto donde se unen dos lados se llama vértice.
La suma de dos lados de un triángulo siempre es mayor que el tercero.
La suma de los ángulos de un triángulo es 180º.
Es muy frecuente clasificar los triángulos por los lados (equilátero,
si tiene los tres lados iguales, isosceles, dos
lados iguales y escaleno, ningun lado igual) y
por los ángulos (rectángulo si tiene un ángulo
de 90º, acutángulo si todos los angulos son
menores de 90º y obtusángulo si tiene un ángulo
mayor de 90º)
Mediana
Es la recta que pasa por un vértice y por el punto medio del lado opuesto.
Hay tres medianas y las tres se cortan en un punto que se llama
centro de gravedad (o baricentro) del triangulo.
Bisectriz
Es la recta que que divide el ángulo en dos partes iguales. Hay tres
bisectrices y se cortan en un punto llamado incentro.
Este punto tiene la particularidad de que haciendo centro en él, podemos
dibujar una circunferencia interior al triángulo y que es tangente a los
tres lados del triangulo.
Mediatriz
Es la recta perpendicular en el punto medio de un segmento. Las
mediatrices de los lados de un triángulo se cortan en un punto llamado
circuncentro. Haciendo centro en este punto,
podemos trazar una circunferencia que pasa por los tres vértices del
triángulo.
Altura
Es la recta que pasa por un vértice y es perpendicular al lado opuesto.
Hay tres alturas y se cortan en un punto llamado
ortocentro.
El triángulo más famoso es es triángulo rectángulo. El lado mayor de un
triángulo rectángulo se llama hipotenusa y los
pequeños, catetos. Este triángulo tiene una
propiedad muy importante: Si construimos unos cuadrados en sus lados, la
suma del área de los cuadrados construidos en los catetos es igual al área
del cuadrado construido en la hipotenusa (escrito de forma matemática:
a2 + b2 =c2).
Superficie de un triángulo:
La fórmula que todos sabemos de la superficie de un triángulo es S = (b.h)/2
Hay otra fórmula menos conocida, la fómula de Herón:
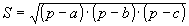
siendo p = (a + b + c)/2
En el plano:
Poligonos: Son figuras geométricas cerradas, formadas por segmentos de
recta.
Si todos los lados y todos los ángulos del poligono son iguales el
poligono se llama poligono regular.
Los polígonos mas importantes son, el triángulo y los cuadrilateros.
Cuadrilateros: Son poligonos que tienen cuatro lados.

Paralelogramos: Son cuadrilateros que tienen sus lados paralelos dos a
dos. Son paralelogramos el rectángulo, el cuadrado y el rombo.
Trapecio: es un cuadrilatero que tiene dos lados paralelos.

Circunferencia: Es una linea cerrada que tiene la propiedad de que todos
los puntos de esa linea estan a la misma distancia de un punto fijo (centro).
El segmento de recta que va desde el centro hasta la circunferencia se
llama radio. El segmento de recta que va desde un punto de la circunferencia
a otro pasando por el centro se llama diámetro.
Las circunferencias tienen una propiedad muy notable: Si medimos la
longitud de una circunferencia y la dividimos por su diámetro siempre da el
mismo número. A ese número le han dado el nombre de p.
La longitud de la circunferencia es 2 pr.
La superficie limitada por la circunferencia se llama círculo. El área
del círculo es p r2.
La ecuación de una circunferencia de centro el origen de coordenadas es:
x2 + y2 =R2.

Elipse: Es una linea cerrada que tiene la propiedad de que la suma de las
distancias a dos puntos dados (focos) es constante.
El segmento de recta que une los dos puntos mas alejados se llama eje
mayor (=2a).
El segmento de recta que une los dos puntos menos alejados se llama eje
menor (=2b).
Centro es el punto de corte de los ejes.
Vértices son los cuatro puntos donde los ejes cortan a la elipse.
Focos son dos puntos, situados en el eje mayor, a igual distancia del
centro y que cumplen la condición de que la suma de las distancias desde
esos puntos a cualquier punto de la elipse, es constante (=2a).
El área de la superficie encerrada por la elipse es p
ab.
La ecuación de una elipse es: x2/a2 + y2/b2
= 1.
En el espacio:
Poliedros: Son cuerpos con todas sus caras planas:

Prisma: Es un poliedro cuyas bases son poligonos iguales y las caras
paralelogramos.
El segmento común a dos caras se llama arista.
Vértice es el punto de unión de dos aristas.
El prisma es recto si las aristas son perpendiculares a la base.
El prisma es regular si es recto y sus bases son ppligonos regulares.
El volumen de un prisma es el área de la base por la altura (V = A.h)
Paralelepipedo: Es un prisma cuyas pases son paralelogramos.
Piramide: Es un poliedro cuya base es un polígono y las caras son
triángulos.
Una piramide es regular si la base es un polígono regular y la altura
pasa por el centro.
El volumen de una piramide es 1/3 A.h.
Una piramide cuyas 4 caras son un triangulo se llama tetraedro.
Un tetraedro regular es un
poliedro regular formado por 4
triángulos equiláteros iguales.
Cuerpos con alguna cara curva:

Cilindro: Es el cuerpo que se genera cuando un segmento de recta se
desplaza apoyandose en dos circunferencias iguales y paralelas.
El volumen de un cilindro es el área de la base por la altura (V = A.h)

Cono: Es el cuerpo que se genera cuando un segmento de recta se desplaza apoyandose en una circunferencia y en un punto (situado en un palno distinto
a la circunferencia).
El volumen de cono es 1/3 A.h.

Esfera: Es la superficie que tiene la propiedad de que todos sus puntos estan a la misma distancia (radio) de un punto (centro).
El área de la esfera es 4 p
r2.
El volumen de la esfera es 4/3p
r3.
La ecuación de una esfera es: x2 + y2 + z2
= r2
Nombres de Polígonos
| Nombre |
Lados |
Ángulos |
| Triángulo |
3 |
3 |
| Cuadrilátero |
4 |
4 |
| Pentágono |
5 |
5 |
| Hexágono |
6 |
6 |
| Heptágono |
7 |
7 |
| Octógono |
8 |
8 |
| Eneágono |
9 |
9 |
| Decágono |
10 |
10 |
Identificar la clase de triángulo según sus lados
Clases de triángulos según
sus lados
-
Un triángulo
RECTANGULO tiene un ángulo de 90o
-
Un triángulo OBTUSO
tiene un ángulo mayor a 90o.
-
Un triángulo AGUDO
tiene todos los ángulos menores a 90o.
Identificar triángulos según sus lados
Clases de triángulos según
sus lados
-
Un triángulo
EQUILATERO tiene los tres lados del mismo largo.
-
Un triángulo ISOSCELES
tiene dos lados con el mismo largo.
-
Un triángulo ESCALENO
tiene los tres lados de largos diferentes.
Encontrar el tercer ángulo de un triángulo
La suma de los ángulos
interiores de un triángulo es igual a 180o. Para
encontrar el tercer ángulo de un triángulo si conoces los
otros dos, debes restarle a 180o la cantidad de
grados de los otros dos ángulos..
Ejemplo: ¿Cuántos grados
tiene el tercer ángulo de un triángulo cuyos otros dos
ángulos son 40o y 65o? Respuesta: 180o
- 40o -65o = 75o
Encontrar el cuarto ángulo de un cuadrilátero
La suma de los ángulos
interiores de un cuadrilátero es igual a 360o.
Para averiguar el cuarto ángulo de un cuadrilátero si
conocemos los otros tres ángulos debes restar a 360o
la cantidad de grados de los otros tres ángulos.
Ejemplo: ¿Cuántos grados
hay en el cuarto ángulo de un cuadrilátero cuyos otros tres
ángulos son 80o and 110o y 95o?
La respuesta: 360o - 80o - 110o
- 95o = 75o
Dos ángulos son
complementarios si la suma de sus grados es igual a 90º.o.
Si conocemos un ángulo, su ángulo complementario se puede
averiguar restando la medida del mismo a 90o.
Ejemplo: ¿Cuál es el
ángulo complementario de 43o?
Solución: 90o - 43o = 47o
Ángulos complementarios o suplementarios
Dos ángulos son
complementarios si la suma de sus ángulos es igual a 90o.
Si conocemos un ángulo, su ángulo complementario se puede
encontrar restando la medida del mismo a 90o.
Ejemplo: ¿Cuál es el
ángulo complementario de 43o?
Solución: 90o - 43o = 47o
Dos ángulos son
suplementarios si la suma de sus grados es igual a 180o.
Si conocemos un ángulo, su ángulo suplementario se puede
averiguar restando la medida del mismo a 180o.
Ejemplo: ¿Cuál es el
ángulo suplementario de 143o?
Solución: 180o - 143o = 37o
Dos ángulos son
suplementarios si la suma de sus grados es igual a 180o.
Si conocemos un ángulo, su ángulo suplementario se puede
averiguar restando la medida del mismo a 180o.
Ejemplo: ¿Cuál es el
ángulo suplementario de 143o?
Solución: 180o - 143o = 37o
Calcular la superficie de un cuadrado
Como averiguar la
superficie de un cuadrado:
-
La superficie de un
cuadrado se puede averiguar multiplicando la base por si
misma. Es similar a la superficie de un rectángulo pero
la base tiene el mismo largo que la altura.
-
Si un cuadrado tiene
una base de 6 Cm, su superficie es 6 X 6= 36 Cm
cuadrados.
Calcular la superficie de un rectángulo
Como averiguar la
superficie de un rectángulo:
-
La superficie de un
rectángulo se puede averiguar multiplicando la Calcular
la superficie de un rectángulo por la altura.
-
Si la base de un
rectángulo mide 6 metros y la altura 4 metros, su
superficie es 6*4=24 metros cuadradas.
Calcula
la superficie de un paralelogramo
Como averiguar la
superficie de un paralelogramo:
-
La superficie de un
paralelogramo se puede averiguar multiplicando la base
por la altura.
-
Si la base de un
paralelogramo mide 6 pulgadas y la altura 4 metros, su
superficie es 6 X 4 = 24 metros cuadrados.
Calcular la superficie del trapeizoide
Un trapeziode es un
cuadrilátero (tiene 4 lados) y tiene solo un par de lados
paralelos.
Como determinar la
superficie de un trapezoide:
-
Sumar los largos de
los 2 lados paralelos
-
Divide por 2 para
sacar el largo promedio de los lados paralelos.
-
Multiplica esto por la
altura (distancia entre los lados paralelos)
Calcular la superficie de un triángulo
Como averiguar la
superficie del triángulo:
-
La superficie del
triángulo se puede averiguar multiplicando la base por
una vez y media la altura.
-
Si un triángulo tiene
una base de 6 metros de largo y una altura de 4 metros,
su superficie es 6 X 2= 12 metros cuadrados.
Encontrar la superficie de un círculo
Como encotrar la
superficie de un círculo:
-
La superficie de un
círculo se puede averiguar multiplicando pi (p =3.14)
por el radio al cuadrado.
-
Si un círculo tiene un
radio de 4, su superficie es 3.14 X 4 X 4= 50.24.
-
Si conoces el diámetro,
el radio es la mitad de su largo.
Calcular el perímetro de un cuadrado
El perímetro de un
cuadrado es la distancia alrededor del cuadrado. Un cuadrado
tiene cuatro lados de igual largo. La fórmula para encontrar
el perímetro de un cuadrado es 4 X (Largo de un Lado).
Calcular el perímetro del rectángulo
El perímetro de un
rectángulo es la distancia alrededor del rectángulo. Un
rectángulo tiene cuatro lados cuyos lados opuestos son
congruentes. La fórmula para averiguar el perímetro es Lado
A + Lado B + Lado A + Lado B. Esto también se podría
enunciar como 2 X lado A + 2 X lado B o 2 X (Lado A + Lado
B)
Calcular el perímetro de un paralelogramo
El perímetro de un
paralelogramo es la distancia alrededor del paralelogramo.
Un paralelogramo tiene cuatro lados cuyos lados opuestos son
congruentes. La fórmula para averiguar el perímetro es Lado
A + Lado B + Lado A + Lado B. Esto también se podría
enunciar como 2 x Lado A + 2 X Lado B o 2 X (Lado A + Lado
B).
Calcular la circunferencia de un círculo
La circunferencia de un
círculo es la distancia alrededor del círculo. Se podría
llamar perímetro del círculo.
Como encontrar la
circunferencia de un círculo:
-
La circunferencia de
un círculo se puede averiguar multiplicando pi ( p=
3.14) por el díametro del círculo.
-
Si un círculo tiene un
diámetro de 4, su circuferencia es 3.14 X 4=12.56
-
Si conoces el radio,
el diámetro es dos veces su largo.
Calcular la superficie de un cubo
Para calcular la
superficie de un cubo, encuentra la superficie de una cara y
multiplícala por 6. La superficie de cualquier lado es el
largo de una cara al cuadrado.
Ejemplo: la superficie de
un cubo cuya cara mide 4 = 4 X 4 X 6 = 96
Superficie de un prisma rectangular
Un prisma rectangular
tiene 2 extremos y cuatro caras. Las caras opuestas tienen
la misma superficie. La superficie es la suma de las
superficies de las seis caras.
Como
encontrar la superficie de un prisma rectangular:
-
Encuentra la
superficie de dos caras (largo X Altura) X 2 lados
-
Encuentra la
superficie de los lados adyacentes (ancho X altura) X 2
lados
-
Encuentra la
superficie de los extremos (largo*ancho) *2 extremos
-
Suma las tres
superficies y encuentra la superficie total.
-
Ejemplo: La superficie
de un prisma rectangular de 5 cm de largo, 3 cm de ancho
y 3 cm de alto = 5 X 2 X 2 + 3 X 2 X 2 + 5 X 3 X 2 = 20
+ 12 + 30 = 62 cm2.
Superficie de cilindros.
Para encontrar la
superficie de un cilindro suma la superficie de cada extremo
más la superficie del lado. La superficie de cada extremo es
p r2. Hay dos extremos por lo tanto su superficie combinada
es 2 p r2. La superficie del lado es la
circunferencia por la altura o 2 p r a.
La formula completa para
la superficie de un cilindro es 2 p r2 + 2 p r a
Volumen
de un cubo
El volumen de un cubo es
(largo de la cara)3.
Volumen
de un prisma rectangular
El volumen de un prisma
rectangular se puede averiguar con la siguiente formula:
volumen = largo * ancho * altura
Volumen
de un Prisma triangular
El volumen de un prisma
triangular se puede averiguar con la siguiente fórmula:
volumen = ½ X largo
X ancho X altura
Volumen
de un cono
El volumen de un cono es
1/3 (Superficie de la base)(altura)= 1/3 p r2 a
Volumen
de un cilindro
El volumen de un cilindro
es igual a (superficie de la base) X altura = p r2
h
Volumen
de una esfera
El volumen de una esfera
se puede averiguar con la siguiente fórmula:
volumen = 4/3 p r3
Volumen
de una pirámide
Una pirámide tiene una
base y caras triangulares que se levantan para unirse en un
mismo vértice. La base puede ser un polígono tal como un
cuadrado, un rectángulo, un triángulo, etc. La formula
general para el volumen de una pirámide es:
Superficie de la base
X Altura X 1/3
El volumen de una pirámide
con base rectangular es igual a:
Largo de base X Ancho de
base X Altura X 1/3
|