L  a  G r a n  E n c i c l o p e d i a   I l u s t r a d a  d e l   P r o y e c t o  S a l ó n  H o g a r

 

El Teorema de Pitágoras

Ver: Triangulos      Teorema de Pitagoras       Conceptos Generales
 

Ya los egipcios en tiempos anteriores a Pitágoras, quien vivió en el siglo VI a.C., conocían la relación que existe entre los tres lados de un triángulo rectángulo cualquiera:

\begin{displaymath} a^2 + b^2 \;=\; c^2 \end{displaymath}

Lo sabían por experiencia, es decir, habían observado que en todos los triángulos rectángulos que ellos habían tenido la ocasión de conocer (tomar sus medidas, en particular) se cumplía la relación.

Sin embargo, nunca se ocuparon de hacer una demostración que explicara por qué, en cualquier triángulo rectángulo, del tamaño y la forma que fuese, esa relación tenía que cumplirse.

Los griegos de la época en que vivía Pitágoras no usaban los símbolos matemáticos como: $+$ , $=$ , $a^2$ , que se usan hoy en día, y su forma de escribir esa relación que hoy se llama Teorema de Pitágoras era esencialmente geométrica: sobre cada uno de los lados de un triángulo rectángulo, construían un cuadrado, como en la figura siguiente:

La igualdad $a^2+b^2=c^2$ que escribimos hoy, ellos la expresaban diciendo que el área del cuadrado construido sobre el lado mayor de un triángulo rectángulo era igual a la suma de las áreas de los cuadrados construidos sobre cada uno de los otros dos lados.

Hay diversas versiones acerca de cómo fue que Pitágoras demostró el teorema que le hizo famoso.

En lo que sigue, se mostrará una de las demostraciones que se cree que dio Pitágoras.

 


Entre los grandes teoremas de toda la historia de la Matemática, ciertamente está el Teorema de Pitágoras.

Tal vez una de las razones que hay para considerarlo así, sea la simplicidad de su enunciado, unida a la inmensa variedad de aplicaciones que tiene.

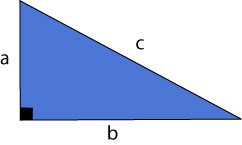
Para comprender lo que enuncia el Teorema de Pitágoras, basta con saber lo que es un triángulo rectángulo, y lo que significa elevar un número al cuadrado.

Si $ABC$ es un triángulo rectángulo, y $\angle\: ACB=90^{\circ}$

 

los lados $AC$ y $CB$ son llamados los catetos (son los lados adyacentes al ángulo recto) y el lado $AB$ es la hipotenusa (el lado opuesto al ángulo recto).

El Teorema de Pitágoras asegura que

\begin{displaymath} (AB)^2 \;=\; (AC)^2+(CB)^2 \end{displaymath}

Es decir, que, en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Se cree que la demostración que hizo Pitágoras de ese teorema es la que se muestra en la figura de la izquierda.

 


El cuadrado $ABCD$ tiene lado igual a $a+b$ . Los triángulos $EFD$ , $FGD$ , $BFH$ y $BFI$ son todos rectángulos y todos tienen catetos $a$ y $b$ y su hipotenusa es igual a $c$ .

Cuando se retiran estos 4 triángulos de la figura anterior, queda una figura de área igual a $a^2+b^2$ (ver figura a la derecha)


Ahora, se vuelven a colocar los 4 triángulos mencionados dentro del cuadrado $ABCD$ , de lado $a+b$ , pero en otra posición. (Figura siguiente).

El cuadrilátero $KIHJ$ es un cuadrado, porque cada uno de sus ángulos internos es igual a $90^{\circ}$ . Esto se deduce de lo siguiente:

Si $\alpha$ y $\beta$ son los ángulos agudos del triángulo $IBH$ , entonces $\alpha+\beta=90^{\circ}$ , porque $\angle IBH=90^{\circ}$ y la suma de los ángulos internos del cualquier triángulo es igual a $180^{\circ}$ .

 

Como $AKI$ y $IBH$ son congruentes entonces $\angle\: AIK=\beta$ . como $\beta+\alpha+\angle\: KIH=180^{\circ}$ , y $\alpha+\beta=90^{\circ}$ , entonces $\angle\: KIH=90^{\circ}$

De la misma manera, se ve que los otros tres ángulos internos del cuadrilátero $KIHJ$ son rectos.

Por lo tanto el área de $KIHJ=c^2$ , porque $c$ es la hipotenusa de los 4 triángulos rectángulos.

Ahora, al retirar los 4 triángulos rectángulos, queda el cuadrado de lado $c$ (ver figura a la izquierda)
 
 
 


De cualquier manera que se retiren los 4 triángulos rectángulos, la figura que se obtiene al final tendrá siempre área igual. Por eso, $a^2+b^2=c^2$ . De esta manera, queda demostrado el Teorema de Pitágoras.

A continuación, se resolverá, usando este teorema, un problema que aparece en un libro del siglo XII d.C., escrito por un gran matemático de la India: Bhaskara Akaria.

Un águila se encontraba en la copa de un árbol en cuya base estaba la cueva de una ardilla. El águila observó a la ardilla parada a 15 m. de distancia de la base del árbol:

 

La ardilla corrió hacia el árbol y el águila avanzó en línea recta hasta alcanzar a la ardilla, antes de que ésta llegara a su cueva. Si la altura del árbol es de 5 metros y la ardilla y el águila recorrieron distancias iguales hasta encontrarse, ¿a cuántos metros de la cueva se encontraron?
 

 
Solución:

Según los datos del problema,

\begin{eqnarray*} AB & = & BC \qquad \mbox{(pues el recorrido del \'{a}guila y ... ...uales)} \\ [.3cm] AD & = & 5 \: m. \\ [.3cm] DC & = & 15 \: m. \end{eqnarray*}
 
pues el recorrido del águila y el de la ardilla son iguales. Se pide calcular $DB$ .

Como$ADB$ es un triángulo rectángulo, con ángulo recto en $D$ , se tiene, por el teorema de Pitágoras, que:

 
\begin{displaymath} (AB)^2 \;=\; (AD)^2 + (DB)^2 \end{displaymath} (1)

Por otra parte,

$DC=DB+BC$ y se sabe que $DC=15\:m$ . Es decir, $BC=15-DB$ .
Como , sustituyendo $AB$ en la igualdad (1) por $BC=15-DB$ :

\begin{eqnarray*} (15-DB)^2 & = & (AD)^2+(DB)^2 \end{eqnarray*}

 
Pero $AD=5$ ; así

 
\begin{eqnarray*} (15-DB)^2 & = & 5^2+(DB)^2 \\ [.3cm] (15)^2-30DB+(DB)^2 & = & 5^2+(DB)^2 \end{eqnarray*}
 

Restando $(DB)^2$ en ambos miembros, se obtiene:
 
\begin{eqnarray*} 225-30DB & = & 25 \\ [.3cm] 200 & = & 30DB \\ [.3cm] \displaystyle \frac{200}{30} & = & DB \end{eqnarray*}
 

 
\begin{displaymath} DB \;=\; \frac{20}{3} \;=\; 6.666\ldots \end{displaymath}

Entonces, la ardilla cayó en las garras del águila cuando le faltaban aún ¡$\;6.666\ldots$ metros para llegar a su cueva !


 


Otro problema del mismo libro de Bhaskara:

Si un bambú de 16 m. de altura se quiebra por el viento de manera tal que la punta toca al suelo a 6 m. de distancia de la base, ¿a qué altura a partir del suelo fue quebrado el bambú ?


 
Sea $x$ la altura que se pide.

Se obtiene un triángulo rectángulo entre los dos trozos de bambú partido y el suelo.

Por el teorema de Pitágoras, se sabe que

\begin{displaymath} x^2+6^2 \;=\; h^2 \end{displaymath}

 
Ahora, $x+h=16$ , porque $x$ y $h$ son las longitudes de los dos pedazos que quedaron del bambú de 16 m. de alto, después de haberse partido.

Entonces $h=16-x$ . Así,

\begin{eqnarray*} x^2+6^2 & = & (16-x)^2 \\ x^2+6^2 & = & (16)^2-32x+x^2 \\ 6^2... ...\\ 32x & = & 220 \\ [.3cm] x & = & \displaystyle \frac{220}{32} \end{eqnarray*}

 
 
Finalmente:
 
\begin{displaymath} x \;=\; \frac{55}{8} \approx 6.8 \end{displaymath}

entonces, el bambú se quebró a 6.8 m. del suelo.

 

 Ver: Triangulos      Teorema de Pitagoras       Conceptos Generales

WWW.PROYECTOSALONHOGAR.COM


Bibliografía recomendada:

Bárcenas, D., Porras, O. (2002) Elementos de Trigonometría.  para la Enseñanza de la Matemática.
Dunham, W. (1994) The Mathematical Universe. New York: John Wiley & Sons, Inc.