L  a  G r a n  E n c i c l o p e d i a   I l u s t r a d a  d e l   P r o y e c t o  S a l ó n  H o g a r

 

Triángulos

Sigue: Teorema de Pitagoras


Eratóstenes vivió en el siglo III a.C. y principios del II en Alejandría, Egipto, ciudad donde se cultivó el estudio de las ciencias y la filosofía con gran esmero, siguiendo la tradición fundada en Atenas.

Sus aportes a la Matemática fueron muy valiosos, conociéndose además sus aptitudes como deportista y dramaturgo. Entre los hallazgos que le dieron fama está el de lograr calcular la longitud de la circunferencia de la Tierra sin más herramientas que un bastón, una cinta para tomar medidas, un buen conocimiento de la geometría y un gran ingenio.

Primero que todo, supuso que los rayos solares inciden paralelamente sobre la Tierra.
 

Luego, observó que en un lugar al borde del río Nilo, llamado Siena, los rayos del sol caían perpendicularmente sobre la Tierra, justo al mediodía del día 21 de Junio, que es el día del Solsticio de Verano (el día más largo del año en el hemisferio norte). A esa hora, las estacas verticales no producían ninguna sombra sobre el suelo.

En ese mismo momento, en Alejandría, al norte de Siena, un palo clavado perpendicularmente en la superficie terrestre, producía una sombra.

Eratóstenes clavó una estaca vertical en Alejandría al mediodía del día del Solsticio de Verano y calculó el ángulo formado por la estaca y los rayos del sol:
 
 


El ángulo calculado fue de $7^{\circ}$ . Al prolongar el segmento de recta que constituye la estaca hacia el centro de la Tierra se obtiene una recta secante a las prolongaciones de los rayos solares paralelos. Eratóstenes sabía que los ángulos alternos internos que se forman entre dos paralelas y una secante, son iguales. Por eso, el ángulo formado entre Alejandría, el centro de la Tierra y Siena, tenía que ser igual a $7^{\circ}$ también.

Ahora bien, Eratóstenes observó que la proporción entre la distancia entre Siena y Alejandría (794 Kms. aproximadamente) y los $7^{\circ}$ que mide el ángulo que le corresponde, debe ser igual a la proporción entre la longitud de la circunferencia completa de la Tierra y los $360^{\circ}$ que mide el ángulo total que le corresponde. Es decir, si $l$ es la longitud de la circunferencia de la Tierra, entonces

\begin{displaymath} \frac{794}{7} = \frac{l}{360} \end{displaymath}

Este cálculo le permitió obtener una medida de 40.834 Kms. (aunque en su época se usaba otra unidad de medida, el stadium, distinto al kilómetro).

La longitud real es de 40.000 Kms. Todavía hoy asombra la exactitud de este resultado obtenido por Eratóstenes.

 

Entre las figuras más simples que se generan a partir de rectas secantes están los triángulos.

Tres rectas secantes dos a dos que no se corten en un único punto, producen un triángulo cuyos vértices son los tres puntos de corte:


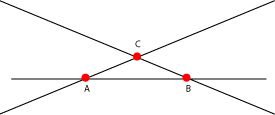Para hacer referencia al triángulo anterior se escribirá $\triangle ABC$ (se lee: triángulo $ABC$ ). También podría escribirse: $\triangle BCA, \triangle CBA$ , etc. El orden en que se dan los vértices no modifica el triángulo.

Se dice que un lado es adyacente a un ángulo si el lado forma parte del ángulo. Por ejemplo, los lados $AB$ y $BC$ son adyacentes al ángulo en $B$ .

Si un lado no es adyacente a un ángulo, se dice que es opuesto a él: el lado $AC$ es opuesto al ángulo en $B$ , que se escribirá así:

\begin{displaymath} \angle\: ABC \qquad\mbox{\'{o}}\qquad \angle\: CBA \end{displaymath}
 

(La letra del medio representa el vértice del ángulo).
 
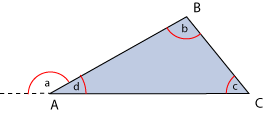
Los ángulos internos del triángulo $ABC$ son:
\begin{displaymath} \angle\: ABC\;,\quad \angle\: BCA\;,\quad \angle\: CAB \end{displaymath}

Los ángulos exteriores son aquellos que se forman entre un lado y la prolongación de otro. Por ejemplo: (ver figura a la derecha)
 
 
 

 

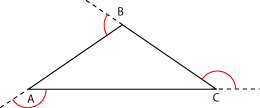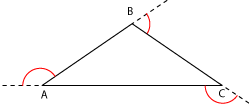Los ángulos dibujados son ángulos exteriores del triángulo $ABC$ . Pero esos no son los únicos ángulos exteriores del triángulo $ABC$ . también lo son los que se muestran a la izquierda.

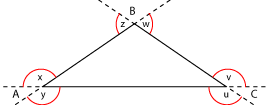Si se dibujan ahora todos los ángulos exteriores al triángulo $ABC$ , se podrá observar algo interesante:

Entre los seis ángulos exteriores que se forman, hay tres parejas de ángulos congruentes (o iguales):
u = v
x = y
z = w

La razón por la cual estos pares de ángulos coinciden, es una de las propiedades fundamentales de los ángulos que se forman entre dos rectas secantes.
 
La prolongación del lado BC y la del lado AC, en ambos sentidos son rectas secantes y los ángulos u y v son opuestos por el vértice. Por lo tanto, son iguales. Lo mismo ocurre con x  y y , z y w. 

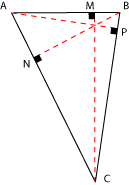
Se distinguen, dentro de un triángulo $ABC$ , cualquiera, algunos segmentos de recta importantes:


Las alturas:

Son los segmentos trazados desde cada vértice, de manera tal que son perpendiculares al lado opuesto. Por ejemplo, los segmentos $AP$ , $CM$ y $BN$ son las tres alturas del triángulo $ABC$ .


 


Las tres alturas se cortan en un punto llamado el ortocentro del triángulo.

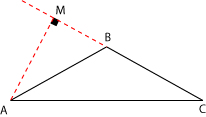
Puede ocurrir que una altura no corte al lado opuesto al vértice de donde parte, sino a una prolongación de ese lado. Por ejemplo: $AM$ es la altura correspondiente al vértice $A$ , del triángulo $ABC$ .

 
Las medianas:

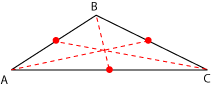
Son los segmentos que unen el punto medio de cada lado con el vértice opuesto. Están trazadas en el siguiente triángulo, las tres medianas.

Las tres medianas de un triángulo cualquiera se cortan en un punto, llamado baricentro, que es el centro de gravedad del triángulo


 
 
Las mediatrices:

La mediatriz del lado $BC$ es la recta perpendicular a $BC$ que pasa por el punto medio de ese segmento.

Así también, las mediatrices de los lados $AB$ y $AC$ son perpendiculares a estos segmentos, que pasan por sus puntos medios.

Las mediatrices se cortan en un punto que es el centro de la circunferencia que pasa por los tres vértices del triángulo (circunferencia circunscrita al triángulo).

Las bisectrices:

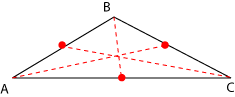
Como su nombre lo indica, son las bisectrices de los tres ángulos interiores.

Las tres bisectrices se cortan en un punto, llamado el incentro del triángulo.


 
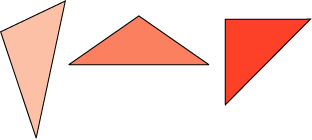
Hay una propiedad que tienen todos los triángulos, y que es muy importante: la suma de los tres ángulos interiores es igual a $180^{\circ}$ .

Esto significa que cualquier triángulo, independientemente de su forma o tamaño, cumple con esa propiedad; por ejemplo, los siguientes triángulos, todos la satisfacen.

 

 

Si se mide con un transportador cada ángulo de un triángulo cualquiera, se constata que, en efecto, la suma de esas medidas es igual a $180^{\circ}$.

Hay una manera de demostrar que esto tiene que ser así, aunque se trate de un triángulo cuyos vértices sean el centro de la Tierra, el centro de la Luna y el centro de Venus, en un instante determinado de sus trayectorias.

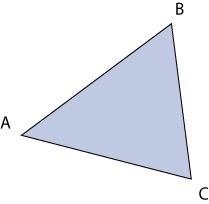
Para demostrarlo, supóngase que se considera el triángulo de la izquierda.

En la demostración se usará sólo el hecho de ser $ABC$ un triángulo, y no alguna propiedad particular de este triángulo.

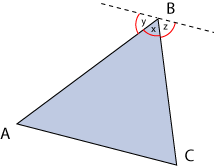
Para comenzar, se escoge un vértice cualquiera, por ejemplo, $B$ , y se traza por $B$ una paralela al lado $AC$ .


 

Como se trata de una recta, la suma $x+y+z$ es igual a $180^{\circ}$ .

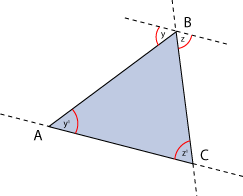
Por otra parte, se tienen dos paralelas cortando a la secante $BC$ (o su prolongación)

 

Como$z$ y $z'$ son ángulos alternos internos, son iguales. Lo mismo se puede decir acerca de los ángulos $y, y'$ . Así, por ser:
\begin{displaymath} x+y+z = 180^{\circ}, \end{displaymath}
 
y puesto que $y=y'$ , $z=z'$ , se tiene que $x+y'+z'=180^{\circ}$ .  

Pero $x$ , $y'$ y $z'$ son los tres ángulos interiores del triángulo $ABC$ . Se ha demostrado, entonces, que la suma de los tres ángulos interiores de un triángulo es igual a $180^{\circ}$ .

 
Demostraremos ahora que todo ángulo exterior a un triángulo es igual a la suma de los dos ángulos interiores no adyacentes. Es decir, si se considera el triángulo:

 

Entonces a = b + c (a es un ángulo exterior y b , c son los ángulos interiores no adyacentes a a).

Se sabe que d + b + c = 180 grados. Por otra parte a + d = 180 grados, por ser a y d adyacentes. Luego,

                           180 grados - d = b + c
                           180 grados - d = a

Esto significa que a = b + c

 

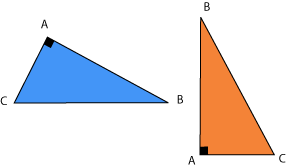
Un triángulo rectángulo es aquel que tiene uno de sus ángulos igual a $90^{\circ}$ . Por ejemplo, los triángulos que se muestran a la derecha son rectángulos. En ambos triángulos, el ángulo en el vértice $A$ es recto.


 
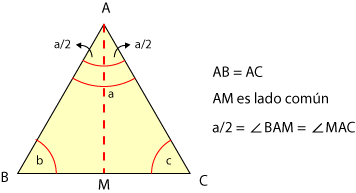
Demostraremos ahora que en un triángulo rectángulo, la suma de los dos ángulos agudos es igual a 90 grados.

Si se tiene un triángulo rectángulo como el siguiente:

 

hay que demostrar que a + b = 90 grados.

se sabe que la suma de los tres ángulos interiores es igual a 180 grados , es decir: a + b + 90 grados = 180 grados. Restando 90 grados a ambos miembros de la igualdad, se obtiene:

                               a + b = 90 grados

 

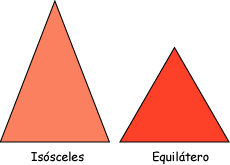Otros triángulos especiales son los siguientes:

  • Triángulo isósceles: cualquier triángulo que tenga sólo dos lados iguales.

  • Triángulo equilátero: cualquier triángulo que tenga los tres lados iguales.

 



 

Congruencia de triángulos.

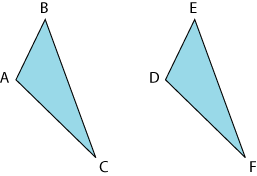
Dos triángulos son congruentes si al hacer una traslación de uno de ellos y colocarlo sobre el otro, es posible hacerles coincidir en todos sus puntos. Por ejemplo, los triángulos de la derecha son congruentes.

No se dice que $ABC$ y $DEF$ son iguales, porque no ocupan la misma posición, pero en realidad la posición es lo único que los diferencia.


Existen ciertos criterios que permiten saber si dos triángulos son congruentes.

 
 
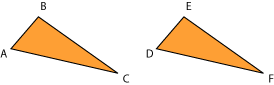1. Criterio de los tres lados:

Dos triángulos son congruentes si cada uno de los tres lados del primero es congruente a uno de los tres lados del segundo. Por ejemplo, en la figura de la izquierda,

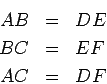
\begin{eqnarray*} AB & = & DE \\ BC & = & EF \\ AC & = & DF \end{eqnarray*}

Este criterio con frecuencia se identifica con las letras LLL (tres lados).

 
2. Criterio de dos lados y el ángulo comprendido entre ellos.

Dos triángulos son congruentes si dos lados del primero y el ángulo comprendido entre esos lados, son congruentes a dos lados del segundo triángulo y el ángulo comprendido entre ellos, respectivamente: (ver figura de la derecha)
 


 
Este criterio se señala con las letras LAL (lado-ángulo-lado).
3. Criterio de dos ángulos y un lado.

Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente congruentes. Por ejemplo, en la figura de la izquierda.

$a=d\;,\quad c=f\qquad$ $\qquad AC=DF$

Este criterio se escribe ALA (ángulo-lado-ángulo).

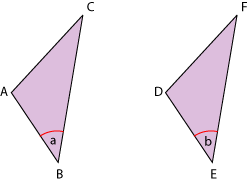
¿Puedes decir que dos triángulos son congruentes, sabiendo sólo que cada ángulo del primero es igual a uno de los ángulos del segundo?

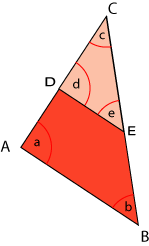
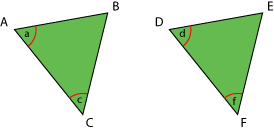
No se puede asegurar que los triángulos sean congruentes en ese caso, porque podría darse la siguiente situación:

 

Los lados DE y AB son paralelos y por lo tanto los ángulos d y a son correspondientes, y también e y b , es decir, d = a y e = b.

Así, los triángulos ABC y DEC tienen los tres ángulos congruentes respectivamente, y sin embargo, ABC y DEC no son congruentes.


 


Se usará ahora el criterio LAL para deducir varias propiedades importantes de los triángulos isósceles:

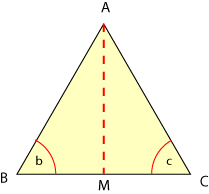
Sea $ABC$ un triángulo isósceles, donde $AB=AC$ y sea $AM$ una bisectriz.

Entonces, se probará que:
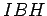1)$AM$ es también la mediana, la altura y la mediatriz.

 
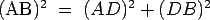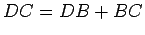2) Los ángulos $b$ y $c$ son congruentes.

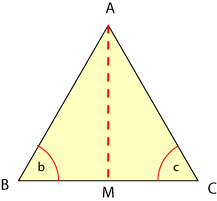
Para ver que $AM$ es la mediana, hay que probar que $M$ es el punto medio de $BC$ , es decir, que $BM=MC$ .

esto será evidente cuando se compruebe que los triángulos $ABM$ y $AMC$ son congruentes.

Como $AM$ es la bisectriz del ángulo $\angle\:BAC$ , entonces los ángulos $\angle\:BAM$ y $\angle\:MAC$ son ambos iguales a la mitad de $\angle\:BAC$ .

$AB=AC$ porque $ABC$ es isósceles y $AM$ es un lado común a los triángulos $ABM$ y $AMC$ .

Usando el criterio LAL, se concluye que estos dos triángulos son congruentes:


 

 

esto significa que $BM=MC$ , y así se obtiene que $AM$ es la mediana sobre el lado $BC$ .

Como$ABM$ y $AMC$ son congruentes, entonces también los ángulos $x$ , $y$ son congruentes.


Pero $x+y=180^{\circ}$ , porque $x$ , $y$ son ángulos adyacentes. Es decir
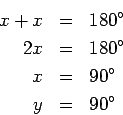
\begin{eqnarray*} x+x & = & 180^{\circ} \\ 2x & = & 180^{\circ} \\ x & = & 90^{\circ} \\ y & = & 90^{\circ} \end{eqnarray*}

esto significa que $AM$ es perpendicular a $BC$ y por eso $AM$ también es la altura y la mediatriz. Con esto queda probada la parte 1).

 

Para probar la parte 2), se usa de nuevo que $ABM$ y $AMC$ son congruentes, y por lo tanto sus tres ángulos tienen que coincidir. Los ángulos en $M$ coinciden, los ángulos en $A$ coinciden y por último, los ángulos en $B$ y $C$ coinciden, es decir, $b=c$ .

Usando la Geometría, Euclides resolvía ecuaciones lineales de una manera muy interesante. Por ejemplo, la ecuación
\begin{displaymath} 2x+\frac{x}{3}+\frac{x}{2} \:=\: 8 \end{displaymath}
 
era interpretada por Euclides de la siguiente manera:

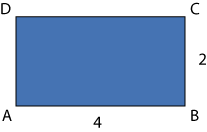
Si se escribe $8=2\cdot 4$ , puede pensarse que 8 es el área de un rectángulo de lados 2 y 4.

 
Por otra parte, la expresión del lado izquierdo de la ecuación se puede escribir como:
\begin{displaymath} \left(2+\frac{1}{3}+\frac{1}{2}\right)\cdot x \:=\: 2x+\frac{x}{3}+\frac{x}{2} \end{displaymath}

también se interpretará esta expresión como el área de un rectángulo con un lado igual a

\begin{displaymath} 2+\frac{1}{3}+\frac{1}{2} \:=\: \frac{17}{6} \end{displaymath}
 
y el otro lado es desconocido: su longitud es la incógnita de la ecuación.

La igualdad

\begin{displaymath} 2x+\frac{x}{3}+\frac{x}{2} \:=\: 8 \end{displaymath}
ó
 
\begin{displaymath} \frac{17}{6}\cdot x \:=\: 2\cdot 4 \end{displaymath}

 
significa, en los términos geométricos de Euclides, que se está buscando un rectángulo que tenga un lado igual a $17/6$ y que su área sea igual a la del rectángulo $ABCD$ .


Como ya se sabe que un lado del rectángulo buscado es $17/6$ basta con encontrar el otro lado.

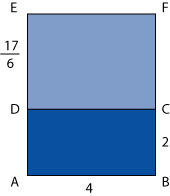
Euclides comienza con la construcción que se muestra en la figura de la izquierda.

 


$DCEF$ tiene lados $4$ y $17/6$ .

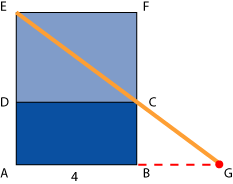
Se traza la diagonal $EC$ y se prolonga hasta cortar la prolongación de $AB$ (ver figura de la derecha).

 

 

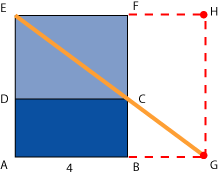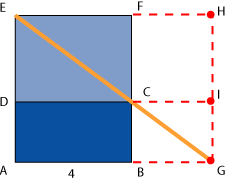
ahora, se construye el rectángulo $AGHE$ (ver figura a la izquierda)

y se prolonga el lado $DC$ .


 

Ver: Triangulos      Teorema de Pitagoras       Conceptos Generales

WWW.PROYECTOSALONHOGAR.COM


Bibliografía recomendada:

Paredes, B., Salcedo, A. (1997) Matemática Santillana, S.A.
Ballester, C. (1995) Geometría. Temas de Matemáticas
Elementales. 2. Caracas: Ediciones CENAMEC.